In figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then angleBAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
To solve the problem step by step, we will analyze the given information and apply the properties of circles and angles.
Step 1: Identify the given information
- We have a circle with a chord AB and a diameter AOC.
- The angle ∠ACB is given as 50°.
- AT is the tangent to the circle at point A.
Step 2: Use the property of angles subtended by the diameter
Since AOC is a diameter, the angle ∠ABC (the angle subtended by the diameter at the circumference) is 90°.
- Therefore, ∠ABC = 90°.
Step 3: Set up the equation for triangle ABC
In triangle ABC, we know that the sum of the angles is 180°.
- So, we can write:
∠ACB+∠ABC+∠CAB=180°
Substituting the known values:
50°+90°+∠CAB=180°
Step 4: Solve for ∠CAB
Now, we can solve for ∠CAB:
∠CAB=180°−50°−90°
∠CAB=40°
Step 5: Relate the angles involving the tangent
Since AT is a tangent to the circle at point A, the angle ∠OAT (where O is the center of the circle) is 90° (the tangent to a circle is perpendicular to the radius at the point of contact).
- Therefore, ∠OAT = 90°.
Step 6: Set up the equation involving angle BAT
Now, we can relate the angles:
∠BAT+∠CAB=90°
Substituting the value of ∠CAB:
∠BAT+40°=90°
Step 7: Solve for ∠BAT
Now, we can solve for ∠BAT:
∠BAT=90°−40°
∠BAT=50°
Conclusion
Thus, the angle ∠BAT is equal to 50°.
Final Answer
Therefore, the answer is (c) 50°.
---
- We have a circle with a chord AB and a diameter AOC.
- The angle ∠ACB is given as 50°.
- AT is the tangent to the circle at point A.
Since AOC is a diameter, the angle ∠ABC (the angle subtended by the diameter at the circumference) is 90°.
- Therefore, ∠ABC = 90°.
In triangle ABC, we know that the sum of the angles is 180°.
- So, we can write:
∠ACB+∠ABC+∠CAB=180°
Substituting the known values:
50°+90°+∠CAB=180°
Now, we can solve for ∠CAB:
∠CAB=180°−50°−90°
∠CAB=40°
Since AT is a tangent to the circle at point A, the angle ∠OAT (where O is the center of the circle) is 90° (the tangent to a circle is perpendicular to the radius at the point of contact).
- Therefore, ∠OAT = 90°.
Now, we can relate the angles:
∠BAT+∠CAB=90°
Substituting the value of ∠CAB:
∠BAT+40°=90°
Now, we can solve for ∠BAT:
∠BAT=90°−40°
∠BAT=50°
Thus, the angle ∠BAT is equal to 50°.
Therefore, the answer is (c) 50°.
Topper's Solved these Questions
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise
32 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Revision Exercise Very Short Answer Question
7 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Long Answer Questions
2 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
10 Videos
Similar Questions
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
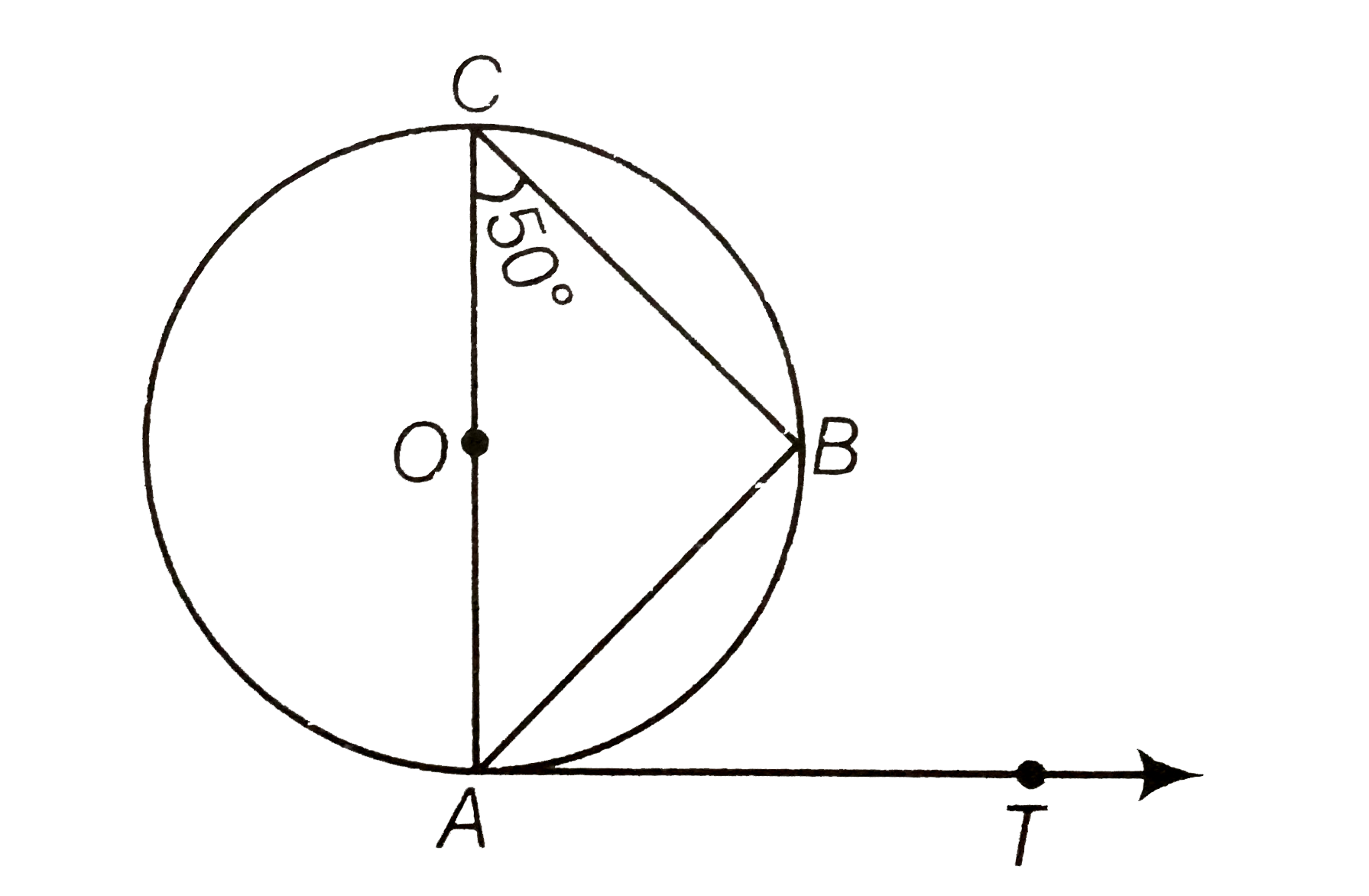
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
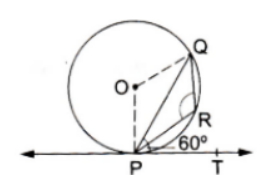
View SolutionIn the adjoining figure, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT=60∘.Find ∠PRQ.
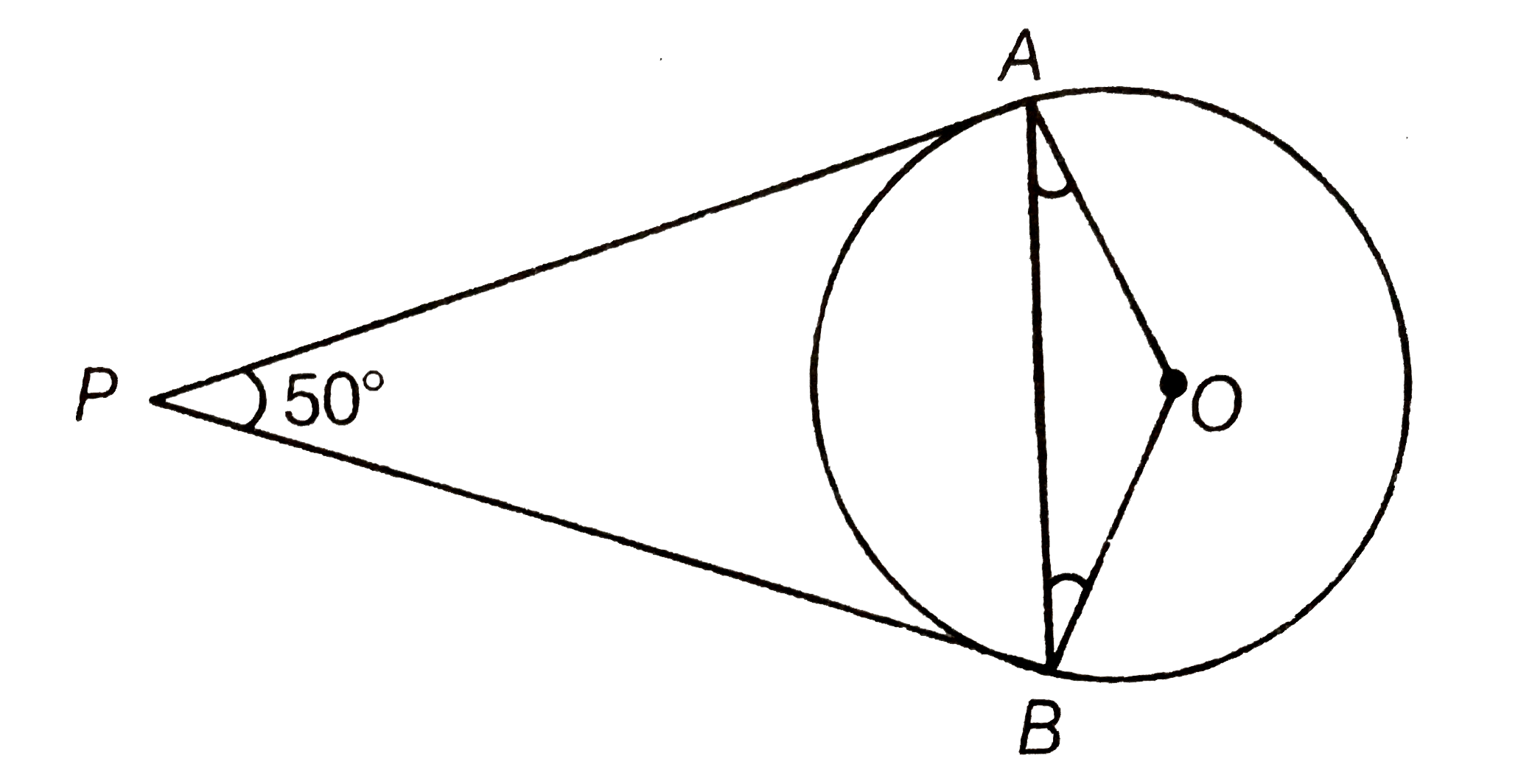
View SolutionIn figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View SolutionIn Figure-2 PQ is tangent to the circle with centre at O , at the point B. If ∠AOB = 100∘ , then ∠ABP is equal to
(A) 50∘
(B) 40∘
(C) 60∘
(D) 80∘
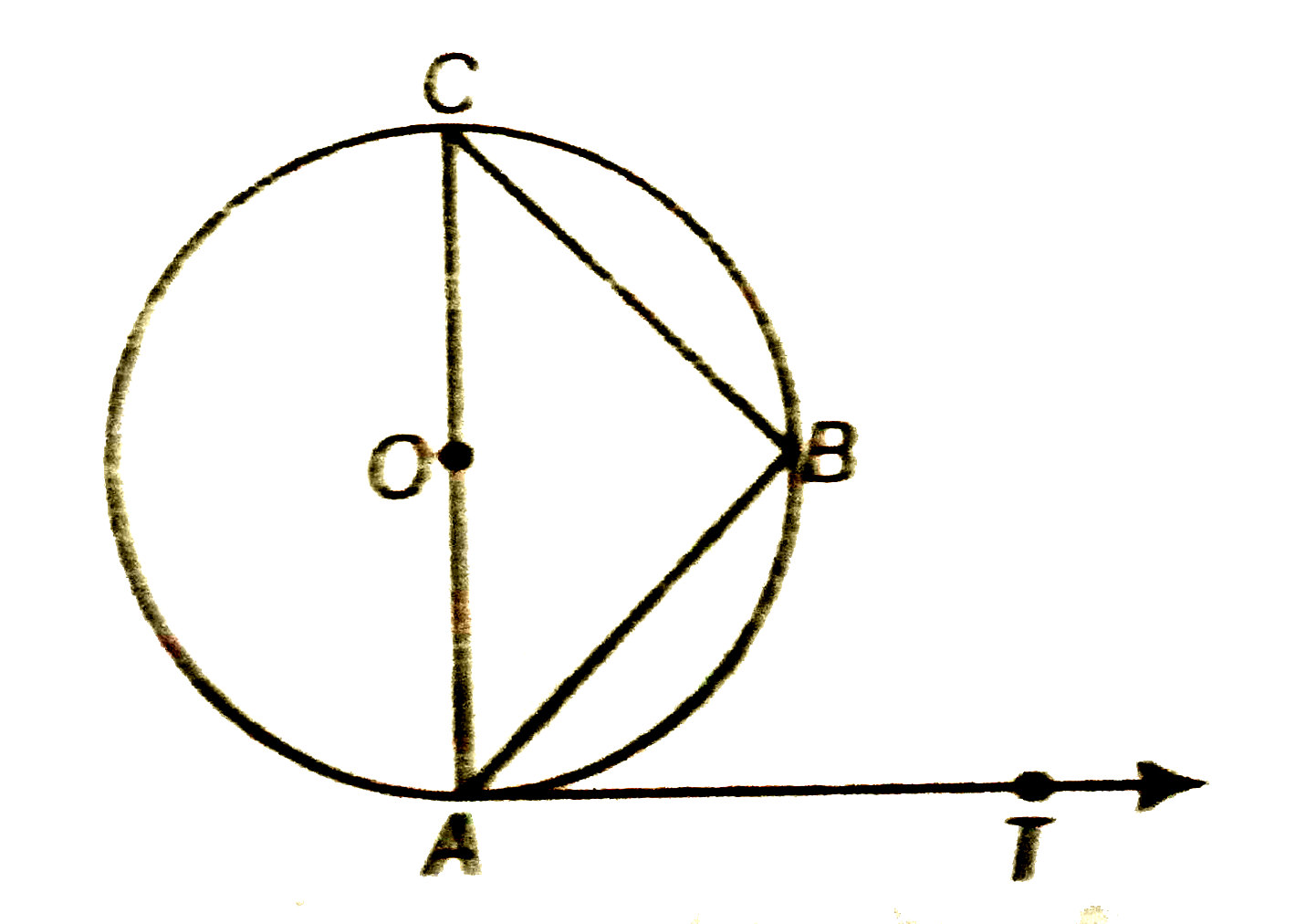
View SolutionIf AB is chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT=∠ACB.
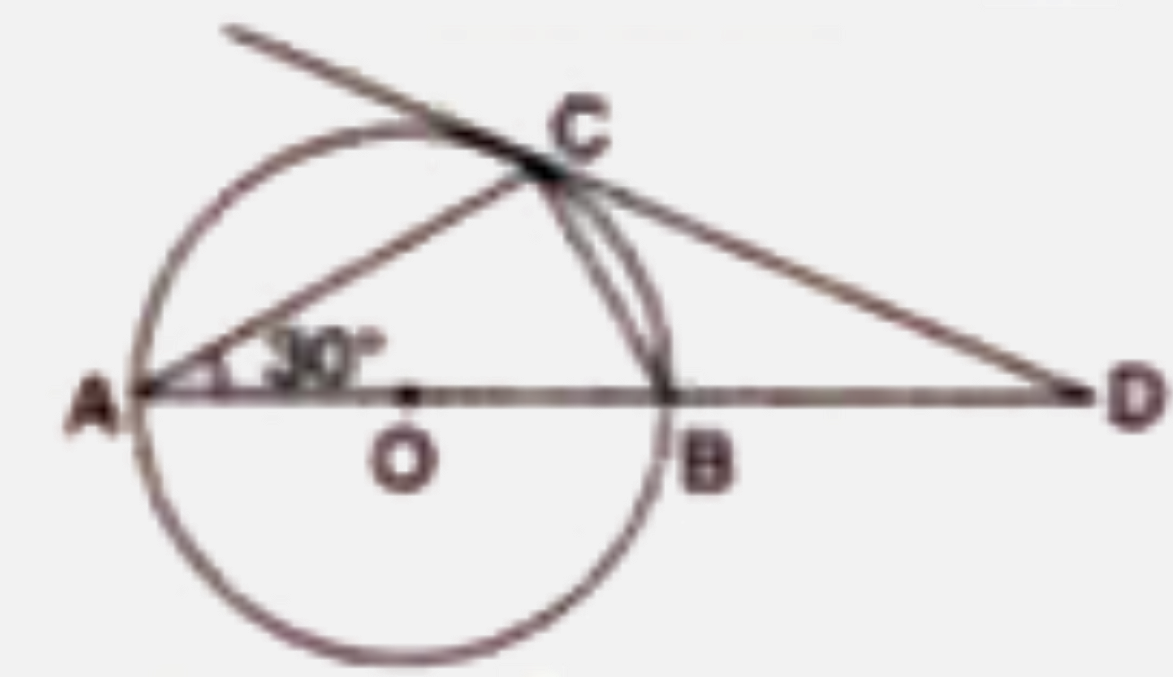
View SolutionIn the given figure AB is the diameter and AC is the chord of a circle such that ∠BAC=30∘. The tangent at C intersects AB produced at D. Prove that :BC=BD.
View SolutionIn figure, BC is a diameter of the circle and ∠BAO=60∘. Then,∠ADCis equal to
View Solution
