An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The othe chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
T1T2(P1V1+P2V2)P1V1T2+P2V2T1
P1V1T1+P2V2T2P1V1+P2V2
P2V2T2+P2V2T1P1V1+P2V2
T1T2(P1V1+P2V2)P1V1T1+P2V2T2
The correct Answer is:A
As no work is done and the system is thermally insulated from the surrounding, the sum of the internal energy of the gas in the two partitions is constant, i.e., U=U1+U2
If both gases have the same degrees of freedom, then
U=f(n1+n2)RT2⇒U1=fn1RT12,U2=fn2RT22
Solving, we get : T=(p1v1+p2v2)T1T2p1v1T2+p2v2T1.
Topper's Solved these Questions
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - Level - 2
40 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Video
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE
1 Video
Similar Questions
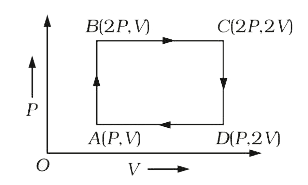
An ideal gas is taken around the cycle ABCDA as shown in the P-V diagram. What is the work done during the cycle?
View SolutionA closed vessel of fixed volume contains a mass m of an ideal gas, the root mean square speed being v. Additional mass m of the same gas is pumped into the vessel and the pressure rises to 2P, the temperature remaining the same as before. The root mean square speed of the molecules now is :
View SolutionTwo particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m/s, their centre of mass has a velocity of 0.5 m/s. When the relative velocity of approach becomes 3m/s, the velocity of the centre of mass is 0.75 m/s.
View SolutionIs it possible to put an artificial satellite in an orbit in such a way that it always remain visible directly over New Delhi ?
View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chmabers has volume V1 and contains ideal gas at pressure P1 and temperature T1.The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View SolutionA container of volume V_(1) has an ideal gas of molar mass M_(1) at pressure P_(1) and temperature T_(1) . Another container of volume V_(2) has another ideal gas of molar mass M_(2) at pres- sure P_(2) and temperature T_(2) . Two gases are mixed in a vessel and acquire an equilibrium temperature and pressure of T_(0) and P_(0) respectively. Find the density of the mixture.
View SolutionTwo thermally insulated vessels are filled with an ideal gas. The pressure, volume and temperature in the two vessels are P_(1), V_(1), T_(1) and P_(2), V_(2), T_(2) respectively. Now, the two vessels are connected using a short insulating tube. (a) Find final temperature of the gas. (b) Express the final pressure of the gas in terms of P_(1), V_(1), P_(2) and V_(2) only.
View SolutionAn ideal gas in thermally insulated vessel at internal (pressure)=P_(1), (volume)=V_(1) and absolute temperature = T_(1) expands irreversiby against zero external, pressure , as shown in the diagram, The final internal pressure, volume and absolute temperature of the gas are p_(2), V_(2) and T_(2) , respectively . For this expansion
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
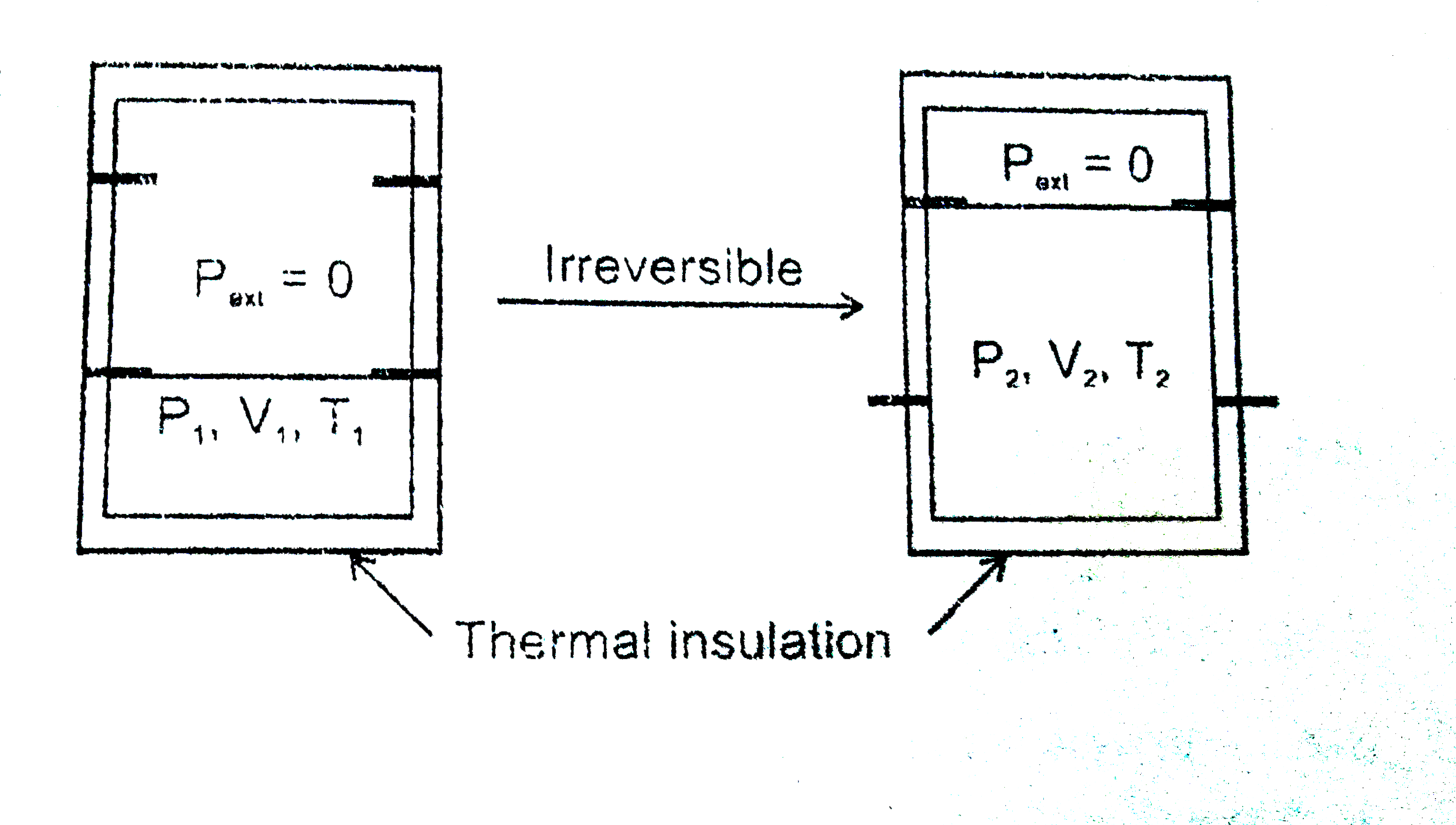
View Solutionगैस से भरे एक ऊष्मारोधी पात्र मेंएक ऊष्मारोधी विभाजक से विभक्त दो प्रकोष्ठ है। एक प्रकोष्ठ का आयतन V1 है तथा उसमें दाब P1 व ताप T1 पर आदर्श गैस भरी है। दूसरे प्रकोष्ठ का आयतन V2 है तथा उसमें दाब P2 व ताप T2 पर आदर्श गैस भरी है। यदि गैस पर बिना कार्य किये विभाजक हटा दिया जाता है तो पात्र में गैस का अन्तिम संतुलन ताप होगा:
View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V_(1) and contains ideal gas at pressure P_(1) and temperature T_(1) . The other chambers has volume V_(2) and contains ideal gas at pressure P_(2) and temperature T_(2) . If the partion is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
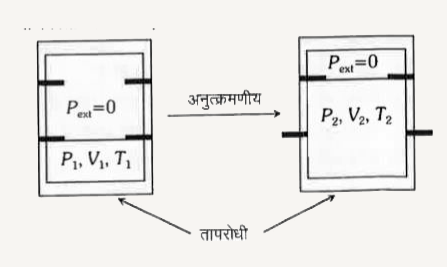
View Solutionऊष्मारोधी बर्तन में एक आदर्श गैस आन्तरिक दाब = P1 आयतन =V1 तथा परमताप = T1 पर शून्य बाह्य दाब के विरूद्ध नीचे दशाये चित्रानुसार अनुत्क्रमणीय प्रसारित होती है। गैस का आखिरी आन्तरिक दाब, आयतन एवं परमताप क्रमशः P2V2 तथा T2 है। इस विस्तारण के लिए
View SolutionOne mole of PCl5 is heated in one litre closed container. If 0.6 mole of chlorine is found at equilibrium, calculate the value of equilibrium constant.
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure = P4, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2andT2, respectively. For this expansion.
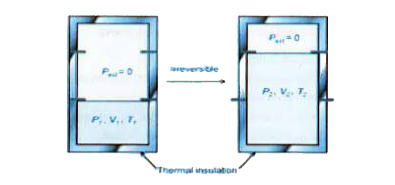
View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V_1 and contains ideal gas at pressure P_1 and temperature T_1 .The other chamber has volume V_2 and contains ideal gas at pressure P_2 and temperature T_2 . If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V_1 and contains ideal gas at pressure P_1 and temperature T_1 .The other chamber has volume V_2 and contains ideal gas at pressure P_2 and temperature T_2 . If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View Solution
