A diatomic ideal gas is used in a Carnot engine as the working substance. If during the adiabatic expansion part of the cycle the volume of the gas increase from V to 32V, the efficiency of the engine is
0.5
0.75
0.99
0.25
The correct Answer is:B
To find the efficiency of a Carnot engine using a diatomic ideal gas during an adiabatic expansion from volume V to 32V, we can follow these steps:
1. Understanding the Carnot Efficiency Formula:
The efficiency η of a Carnot engine is given by the formula:
η=1−T2T1
where T1 is the temperature of the hot reservoir and T2 is the temperature of the cold reservoir.
2. Using the Adiabatic Process Relation:
For an adiabatic process involving an ideal gas, the relationship between temperature and volume is given by:
TVγ−1=constant
where γ (gamma) is the heat capacity ratio. For a diatomic gas, γ=75=1.4.
3. Setting Up the Equation:
Let V1=V and V2=32V. According to the adiabatic relation:
T1Vγ−11=T2Vγ−12
Substituting the values:
T1Vγ−1=T2(32V)γ−1
4. Simplifying the Equation:
We can simplify this equation:
T1Vγ−1=T2(32γ−1Vγ−1)
Dividing both sides by Vγ−1:
T1=T2⋅32γ−1
5. Substituting the Value of γ:
Now substituting γ=75:
T1=T2⋅3275−1
Simplifying 75−1=25:
T1=T2⋅3225
6. Calculating 3225:
We know 32=25, so:
3225=(25)25=22=4
Therefore:
T1=4T2
7. Finding the Efficiency:
Now substituting T1 back into the efficiency formula:
η=1−T2T1=1−T24T2=1−14=34
8. Final Answer:
Thus, the efficiency of the engine is:
η=0.75
The efficiency η of a Carnot engine is given by the formula:
η=1−T2T1
where T1 is the temperature of the hot reservoir and T2 is the temperature of the cold reservoir.
For an adiabatic process involving an ideal gas, the relationship between temperature and volume is given by:
TVγ−1=constant
where γ (gamma) is the heat capacity ratio. For a diatomic gas, γ=75=1.4.
Let V1=V and V2=32V. According to the adiabatic relation:
T1Vγ−11=T2Vγ−12
Substituting the values:
T1Vγ−1=T2(32V)γ−1
We can simplify this equation:
T1Vγ−1=T2(32γ−1Vγ−1)
Dividing both sides by Vγ−1:
T1=T2⋅32γ−1
Now substituting γ=75:
T1=T2⋅3275−1
Simplifying 75−1=25:
T1=T2⋅3225
We know 32=25, so:
3225=(25)25=22=4
Therefore:
T1=4T2
Now substituting T1 back into the efficiency formula:
η=1−T2T1=1−T24T2=1−14=34
Thus, the efficiency of the engine is:
η=0.75
Topper's Solved these Questions
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - Level - 2
40 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE
1 Videos
Similar Questions
A monoatomic ideal gas is used in a carnot engine as the working substance. If during the adiabatic expansion the volume of the gas increases from V8 to V, the efficiency of the engine is
View SolutionDuring an adiabatic reversibly expansion of an ideal gas
View SolutionA diatomic gas is used in car not heat engine having efficiency 80% . Find the ratio of initial volume to final volume of gas during adiabatic expansion.
View SolutionDuring adiabatic expansion of ideal gas, which is correct ?
View SolutionConsider an ideal gas confined in an isolated closed chamber. As the gas undergoes an adiabatic expansion, the average time of collision between molecules increase as Vq, where V is the volume of the gas. The value of q is : (γ=CpCv)
View SolutionAn engine operates by taking a monatomic ideal gas through the cycle shown in the figure. The percentage efficiency of the engine is close to ____________
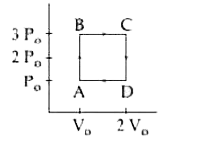
View SolutionA cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in figure.

A to B volume constant, B to C adiabatic, C to D volume constant and D to A adiabatic
VC=VD=2VA=2VB
(a) In which part of the cycle heat is supplied to the engine form outside?
(b) In which part of the cycle heat is being given to the surrounding by the engine ?
(c ) What is the work done by the engine in one cycle ? Write your answer in term of pA,pB,VA ?
(d) What is the efficiency of the engine ?
(γ=53 for the gas), (CV=32R for one mole )
View SolutionAssertion:- During adiabatic expansion of an ideal gas, temperature falls but entropy remains constant.
Reason:- During adiabatic expansion, work is done by the gas using a part of internal energy and no heat exchange teakes place the system and the surrounding.
View SolutionThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as T∝V−34, then the value of CPCV for the gas is
View SolutionAn ideal gas A and a real gas B have their volumes increases from V→2V under isothermal condtitions. The increase in internal energy
View Solution
