A container with insulating walls is divided into two equal parts by a partition fitted with a valve. One part is filled with an ideal gas at a pressure P and temperature T, whereas the other part is completely evacuated . If the valve is suddenly opened, the pressure and temperature of the gas will be
P2,T
P2,T2
P,T
P,T2
The correct Answer is:A
To solve the problem step-by-step, we can follow these logical steps:
Step 1: Understand the Initial Conditions
We have a container divided into two equal parts. One part contains an ideal gas at pressure P and temperature T, while the other part is a vacuum (pressure = 0).
Step 2: Analyze the Process When the Valve is Opened
When the valve is suddenly opened, the gas will expand to fill the entire volume of the container. Since the walls are insulating, no heat can enter or leave the system, indicating that the process is adiabatic.
Step 3: Apply the First Law of Thermodynamics
For an adiabatic process involving an ideal gas, the internal energy remains constant if there is no heat transfer and no work done on or by the system. Therefore, the internal energy before and after the expansion must be the same:
U1=U2
Since the internal energy of an ideal gas is a function of temperature, this implies that:
T1=T2
Thus, the temperature of the gas after the expansion remains T.
Step 4: Use Boyle's Law to Find the New Pressure
Since the process is isothermal (temperature remains constant), we can apply Boyle's Law, which states:
P1V1=P2V2
Where:
- P1=P (initial pressure)
- V1=V2 (initial volume of gas)
- V2=V (final volume of gas after expansion)
Substituting these values into Boyle's Law gives:
P(V2)=P2(V)
Step 5: Solve for the Final Pressure P2
Rearranging the equation to solve for P2:
P2=P(V2)V=P2
Conclusion
After the valve is opened, the pressure of the gas will be P2 and the temperature will remain T.
Final Answer
- Pressure P2=P2
- Temperature T2=T
We have a container divided into two equal parts. One part contains an ideal gas at pressure P and temperature T, while the other part is a vacuum (pressure = 0).
When the valve is suddenly opened, the gas will expand to fill the entire volume of the container. Since the walls are insulating, no heat can enter or leave the system, indicating that the process is adiabatic.
For an adiabatic process involving an ideal gas, the internal energy remains constant if there is no heat transfer and no work done on or by the system. Therefore, the internal energy before and after the expansion must be the same:
U1=U2
Since the internal energy of an ideal gas is a function of temperature, this implies that:
T1=T2
Thus, the temperature of the gas after the expansion remains T.
Since the process is isothermal (temperature remains constant), we can apply Boyle's Law, which states:
P1V1=P2V2
Where:
- P1=P (initial pressure)
- V1=V2 (initial volume of gas)
- V2=V (final volume of gas after expansion)
P(V2)=P2(V)
Rearranging the equation to solve for P2:
P2=P(V2)V=P2
After the valve is opened, the pressure of the gas will be P2 and the temperature will remain T.
- Pressure P2=P2
- Temperature T2=T
Topper's Solved these Questions
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:Level - 2
Explore 40 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
Explore 1 Video
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) TRUE/FALSE
Explore 1 Video
Similar Questions
An ideal gas has pressure P, volume V and temperature T. Select the correct option.
View SolutionA nonconducting cylinder having volume 2V0 is partitioned by a fixed non conducting wall in two equal part. Partition is attached with a valve. Right side of the partition is a vacuum and left part is filled with a gas having pressure and temperature P0 and T0 respectively. If valve is opened find the final pressure and temperature of the two parts.
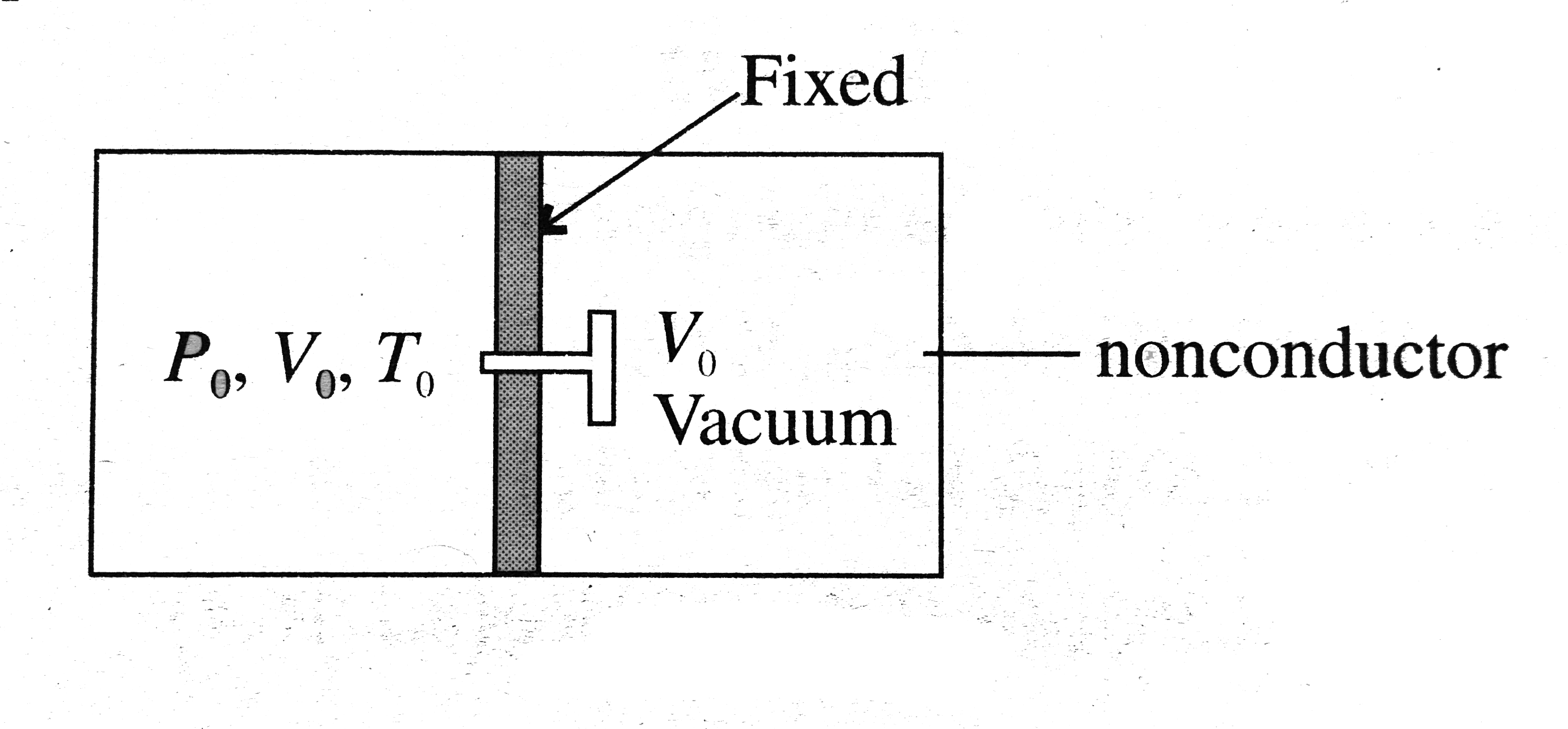
View SolutionA non-conducting cylinder having volume 2V0 is partitioned by a fixed non conducting wall in two equal part. Partition is attached with a valve. Right side of the partition is a vacuum and left part is filled with a gas having pressure and temperature P0 and T0 respectively. If valve is opened find the final pressure and temperature of the two parts.
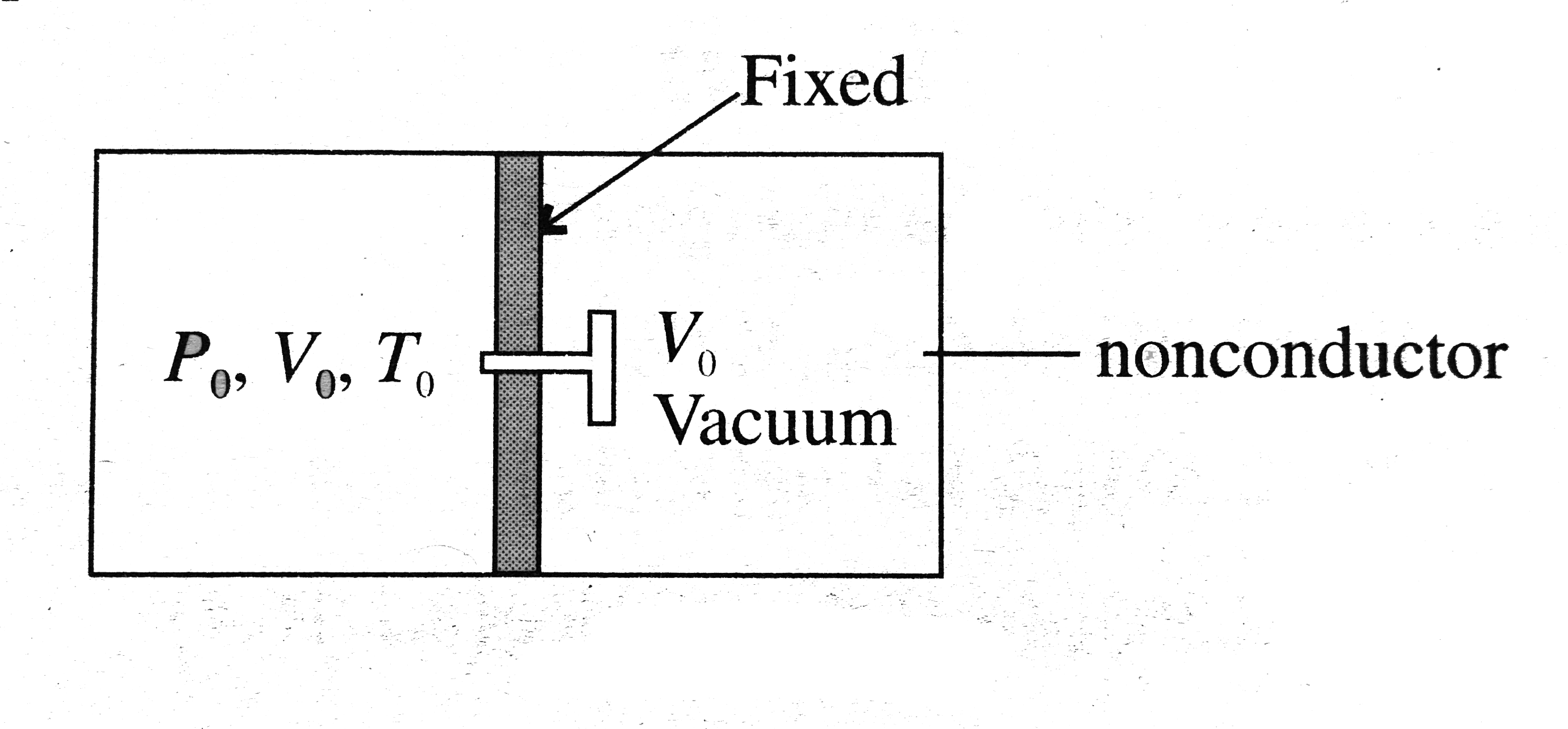
View SolutionA given quantity of a ideal gas is at pressure P and absolute temperature T. The isothermal bulk modulus of the gas is
View SolutionA given quantity of a ideal gas is at pressure P and absolute temperature T. The isothermal bulk modulus of the gas is
View SolutionAn insulated container is divided into two equal portions. One portion contains as ideal gas at pressure P and tenperature T. The othe portion is a perfect vaccume. If a hole is opened between the two portions, claculate
a. the change in internal energy.
b. the change in temperature.
View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1.The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1.The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View SolutionA container of volume 1m3 is divided into two equal parts by a partition. One part has an ideal gas at 300K and the other part is vacuum. The whole system is thermally isolated from the surroundings. When the partition is removed, the gas expands to occupy the whole volume. Its temperature will now be .......
View SolutionA container of volume 1m3 is divided into two equal parts by a partition. One part has an ideal gas at 300K and the other part is vacuum. The whole system is thermally isolated from the surroundings. When the partition is removed, the gas expands to occupy the whole volume. Its temperature will now be .......
View Solution
