An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1.The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
T1T2(p1V1+p2V2)p1V1T2+p2V2T1
p1V1T1+p2V2T2p1V1+p2V2
p1V1T2+p2V2T1p1V1+p2V2
T1T2(p1V1+p2V2)p1V1T1+p2V2T2
The correct Answer is:A
To find the final equilibrium temperature T of the gas in the insulated container after the partition is removed, we can follow these steps:
Step 1: Understand the System
We have an insulated container divided into two chambers:
- Chamber 1: Volume V1, Pressure P1, Temperature T1
- Chamber 2: Volume V2, Pressure P2, Temperature T2
Since the container is insulated, there is no heat exchange with the surroundings (ΔQ=0).
Step 2: Apply the First Law of Thermodynamics
The first law of thermodynamics states:
ΔU=Q−W
Since Q=0 (no heat exchange) and W=0 (no work done), we have:
ΔU=0
This means that the change in internal energy of the system is zero.
Step 3: Write the Expression for Internal Energy
The internal energy change can be expressed as:
ΔU=Ufinal−Uinitial=0
For the two chambers, the internal energy can be written as:
Uinitial=n1CVT1+n2CVT2
Where n1 and n2 are the number of moles in each chamber, and CV is the molar specific heat at constant volume.
Step 4: Express Moles in Terms of Pressure, Volume, and Temperature
Using the ideal gas equation PV=nRT, we can express the number of moles:
n1=P1V1RT1,n2=P2V2RT2
Step 5: Substitute into the Internal Energy Equation
Substituting n1 and n2 into the internal energy equation gives:
Uinitial=(P1V1RT1)CVT1+(P2V2RT2)CVT2
This simplifies to:
Uinitial=P1V1CVR+P2V2CVR
Step 6: Write the Final Internal Energy Expression
After the partition is removed, the total number of moles is n1+n2 and the final temperature is T:
Ufinal=(n1+n2)CVT
Substituting n1+n2:
Ufinal=(P1V1RT1+P2V2RT2)CVT
Step 7: Set Initial and Final Internal Energies Equal
Since Uinitial=Ufinal:
P1V1CVR+P2V2CVR=(P1V1RT1+P2V2RT2)CVT
Step 8: Cancel CV and Rearrange
Cancel CV from both sides:
P1V1R+P2V2R=(P1V1RT1+P2V2RT2)T
Multiply through by R:
P1V1+P2V2=(P1V1T1+P2V2T2)T
Step 9: Solve for Final Temperature T
Rearranging gives:
T=P1V1T2+P2V2T1P1V1+P2V2
Final Answer
The final equilibrium temperature T is:
T=T1T2(P1V1+P2V2)P1V1T2+P2V2T1
We have an insulated container divided into two chambers:
- Chamber 1: Volume V1, Pressure P1, Temperature T1
- Chamber 2: Volume V2, Pressure P2, Temperature T2
The first law of thermodynamics states:
ΔU=Q−W
Since Q=0 (no heat exchange) and W=0 (no work done), we have:
ΔU=0
This means that the change in internal energy of the system is zero.
The internal energy change can be expressed as:
ΔU=Ufinal−Uinitial=0
For the two chambers, the internal energy can be written as:
Uinitial=n1CVT1+n2CVT2
Where n1 and n2 are the number of moles in each chamber, and CV is the molar specific heat at constant volume.
Using the ideal gas equation PV=nRT, we can express the number of moles:
n1=P1V1RT1,n2=P2V2RT2
Substituting n1 and n2 into the internal energy equation gives:
Uinitial=(P1V1RT1)CVT1+(P2V2RT2)CVT2
This simplifies to:
Uinitial=P1V1CVR+P2V2CVR
After the partition is removed, the total number of moles is n1+n2 and the final temperature is T:
Ufinal=(n1+n2)CVT
Substituting n1+n2:
Ufinal=(P1V1RT1+P2V2RT2)CVT
Since Uinitial=Ufinal:
P1V1CVR+P2V2CVR=(P1V1RT1+P2V2RT2)CVT
Cancel CV from both sides:
P1V1R+P2V2R=(P1V1RT1+P2V2RT2)T
Multiply through by R:
P1V1+P2V2=(P1V1T1+P2V2T2)T
Rearranging gives:
T=P1V1T2+P2V2T1P1V1+P2V2
The final equilibrium temperature T is:
T=T1T2(P1V1+P2V2)P1V1T2+P2V2T1
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - Advancel Level Problems
1 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - SUBJECTIVE QUESTIONS
27 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - PART - I
18 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCE ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
64 Videos
Similar Questions
An ideal gas has pressure P, volume V and temperature T. Select the correct option.
View SolutionTwo adiabatic containers have volumes V1 and V2 respectively. The first container has monoatomic gas at pressure p1 and temperature T1. The second container has another monoatomic gas at pressure p2 and temperature T2. When the two containers are connected by a narrow tube, the final temperature and pressure of the gases in the containers are P and T respectively. Then
View SolutionA uniform tube of volume V contains an ideal monatomic gas at a uniform pressure P the temperature of the gas varies linearly along te length of the tube ad T and 2 T are the temperature at the ends.
View SolutionA container with insulating walls is divided into two equal parts by a partition fitted with a valve. One part is filled with an ideal gas at a pressure P and temperature T, whereas the other part is completely evacuated . If the valve is suddenly opened, the pressure and temperature of the gas will be
View SolutionA container with insulating walls is divided into two equal parts by a partition fitted with a valve. One part is filled with an ideal gas at a pressure P and temperature T, whereas the other part is completely evacuated . If the valve is suddenly opened, the pressure and temperature of the gas will be
View SolutionFigure shows volume - temperature (V-T) graph for same mass of an ideal gas at two different pressures P1and P2. Hence
View SolutionSome ideal monoatomic gas A in an enclosure has a pressure P and the temperature T . Another ideal monoatomic gas B enclosed in a container of the same volume has a pressure of 2P and temperature T2. The ratio of the average kinetic energy per molecule of gas A to gas B is
View SolutionFollowing figure shows on adiabatic cylindrical container of volume V0 divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (Cp/Cy=λ) is at pressure P1 and temperature T1 in left part and gas at pressure P2 and temperature T2 in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)

View SolutionAn inflated rubber ballon contains one mole of an ideal gas , has a pressure P, volume V and temperature T. If the temperature rises to 1.1 T, and the volume isincreased to 1.05 V, the final pressure will be
View SolutionThe container shown in figure has two chambers separated by a partition of volumes V1=2.0L and V2=3.0L. The chambers contain μ14.0 and μ2=5.0 mole of a gas at pressure p1=1.00 atm and P2=2.00 atm. Calculate the pressure after the partition is removed and the mixture attains equilibrium.
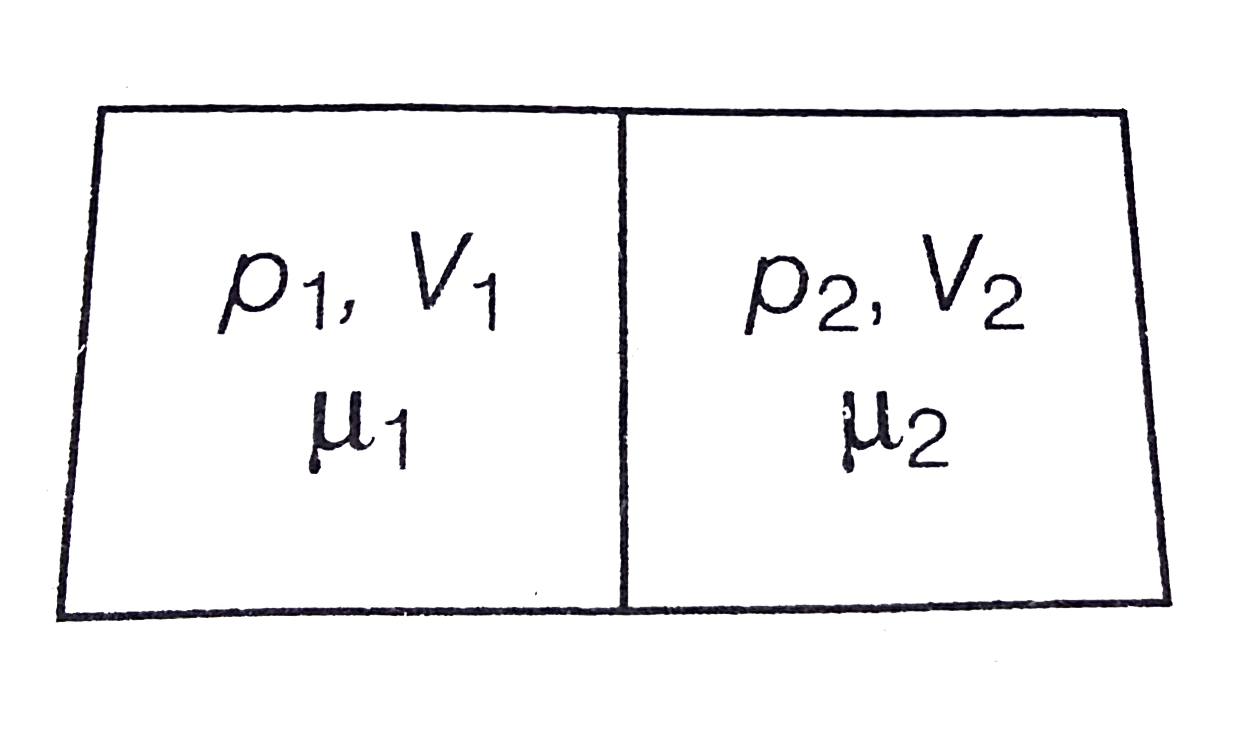
View Solution
