A uniform tube of volume V contains an ideal monatomic gas at a uniform pressure P the temperature of the gas varies linearly along te length of the tube ad T and 2 T are the temperature at the ends.
The number of moles of the gas in the tube is PVRTln2
The number of moles of the gas in the tube is PVRTln4
The internal energy of the gas in the tube is (3/2)PV
The internal energy of the gas in the tube is (3/2)nRT.
The correct Answer is:A, C
To solve the problem, we need to determine the number of moles of the ideal monatomic gas in the tube and the internal energy of the gas. Let's break this down step by step.
Step 1: Understand the Temperature Variation
The problem states that the temperature varies linearly along the length of the tube, with temperatures T at one end and 2T at the other end.
Step 2: Relate Temperature to Length
Let L be the length of the tube. The temperature T′ at a distance x from the end with temperature T can be expressed as:
T′=T+(2T−TL)x=T+TLx
This simplifies to:
T′=T+TLx
Step 3: Ideal Gas Law
Using the ideal gas equation:
PV=nRT
We can express the number of moles n as:
n=PVRT
For a small section of the tube of length dx, the number of moles dN in that section can be expressed as:
dN=P⋅A⋅dxR⋅T′
where A is the cross-sectional area of the tube.
Step 4: Substitute for dx
From the temperature equation, we can differentiate to find dx in terms of dT′:
dT′dx=TL⟹dx=LTdT′
Step 5: Substitute dx into the Number of Moles Equation
Substituting dx into the expression for dN:
dN=P⋅AR⋅T′⋅LTdT′
This simplifies to:
dN=P⋅A⋅LR⋅T⋅1T′dT′
Step 6: Integrate to Find Total Moles
To find the total number of moles N, we integrate dN from T to 2T:
N=∫2TTP⋅A⋅LR⋅T⋅1T′dT′
This integral evaluates to:
N=P⋅A⋅LR⋅Tln(2TT)=P⋅A⋅LR⋅Tln(2)
Step 7: Relate Volume to Area and Length
Since V=A⋅L, we can substitute A⋅L with V:
N=PVRTln(2)
Step 8: Calculate Internal Energy
The internal energy U of an ideal monatomic gas is given by:
U=32nRT
Substituting n from our previous result:
U=32(PVRTln(2))RT=32PVln(2)
Final Results
1. The number of moles of the gas is:
N=PVRTln(2)
2. The internal energy of the gas is:
U=32PVln(2)
The problem states that the temperature varies linearly along the length of the tube, with temperatures T at one end and 2T at the other end.
Let L be the length of the tube. The temperature T′ at a distance x from the end with temperature T can be expressed as:
T′=T+(2T−TL)x=T+TLx
This simplifies to:
T′=T+TLx
Using the ideal gas equation:
PV=nRT
We can express the number of moles n as:
n=PVRT
For a small section of the tube of length dx, the number of moles dN in that section can be expressed as:
dN=P⋅A⋅dxR⋅T′
where A is the cross-sectional area of the tube.
From the temperature equation, we can differentiate to find dx in terms of dT′:
dT′dx=TL⟹dx=LTdT′
Substituting dx into the expression for dN:
dN=P⋅AR⋅T′⋅LTdT′
This simplifies to:
dN=P⋅A⋅LR⋅T⋅1T′dT′
To find the total number of moles N, we integrate dN from T to 2T:
N=∫2TTP⋅A⋅LR⋅T⋅1T′dT′
This integral evaluates to:
N=P⋅A⋅LR⋅Tln(2TT)=P⋅A⋅LR⋅Tln(2)
Since V=A⋅L, we can substitute A⋅L with V:
N=PVRTln(2)
The internal energy U of an ideal monatomic gas is given by:
U=32nRT
Substituting n from our previous result:
U=32(PVRTln(2))RT=32PVln(2)
1. The number of moles of the gas is:
N=PVRTln(2)
2. The internal energy of the gas is:
U=32PVln(2)
Similar Questions
An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1.The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View SolutionAn insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1.The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
View SolutionAn ideal gas has pressure P, volume V and temperature T. Select the correct option.
View SolutionIf 2 mol of an ideal monatomic gas at temperature T0 are mixed with 4 mol of another ideal monatoic gas at temperature 2T0 then the temperature of the mixture is
View SolutionIf 2 mol of an ideal monatomic gas at temperature T0 are mixed with 4 mol of another ideal monatoic gas at temperature 2T0 then the temperature of the mixture is
View SolutionTwo adiabatic containers have volumes V1 and V2 respectively. The first container has monoatomic gas at pressure p1 and temperature T1. The second container has another monoatomic gas at pressure p2 and temperature T2. When the two containers are connected by a narrow tube, the final temperature and pressure of the gases in the containers are P and T respectively. Then
View SolutionThe specific heat of an ideal gas varies with temperature T as
View SolutionA cylindrical tube with adiabatic walls having volume 2V0contains an ideal monoatomic gas as shown in figure. The tube is divided into two equal parts by a fixed super conducting wall. Initially, the pressure and the temperature are P0,T0 on the left and 2P0,2T0 on the rigid. When system is left for sufficient amount of time the temperature on both sides becomes equal

View SolutionTwo closed bulbs of equal volume (V) containing an ideal gas initially at pressure Pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below . The temperature of one of the bulbs is then raised to T2 . the final pressure Pf is
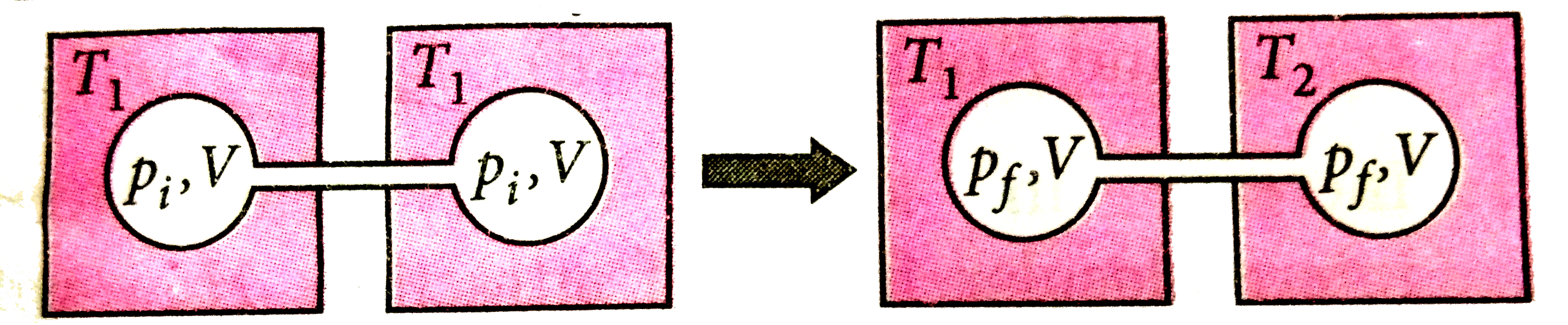
View SolutionSome ideal monoatomic gas A in an enclosure has a pressure P and the temperature T . Another ideal monoatomic gas B enclosed in a container of the same volume has a pressure of 2P and temperature T2. The ratio of the average kinetic energy per molecule of gas A to gas B is
View Solution

