An ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
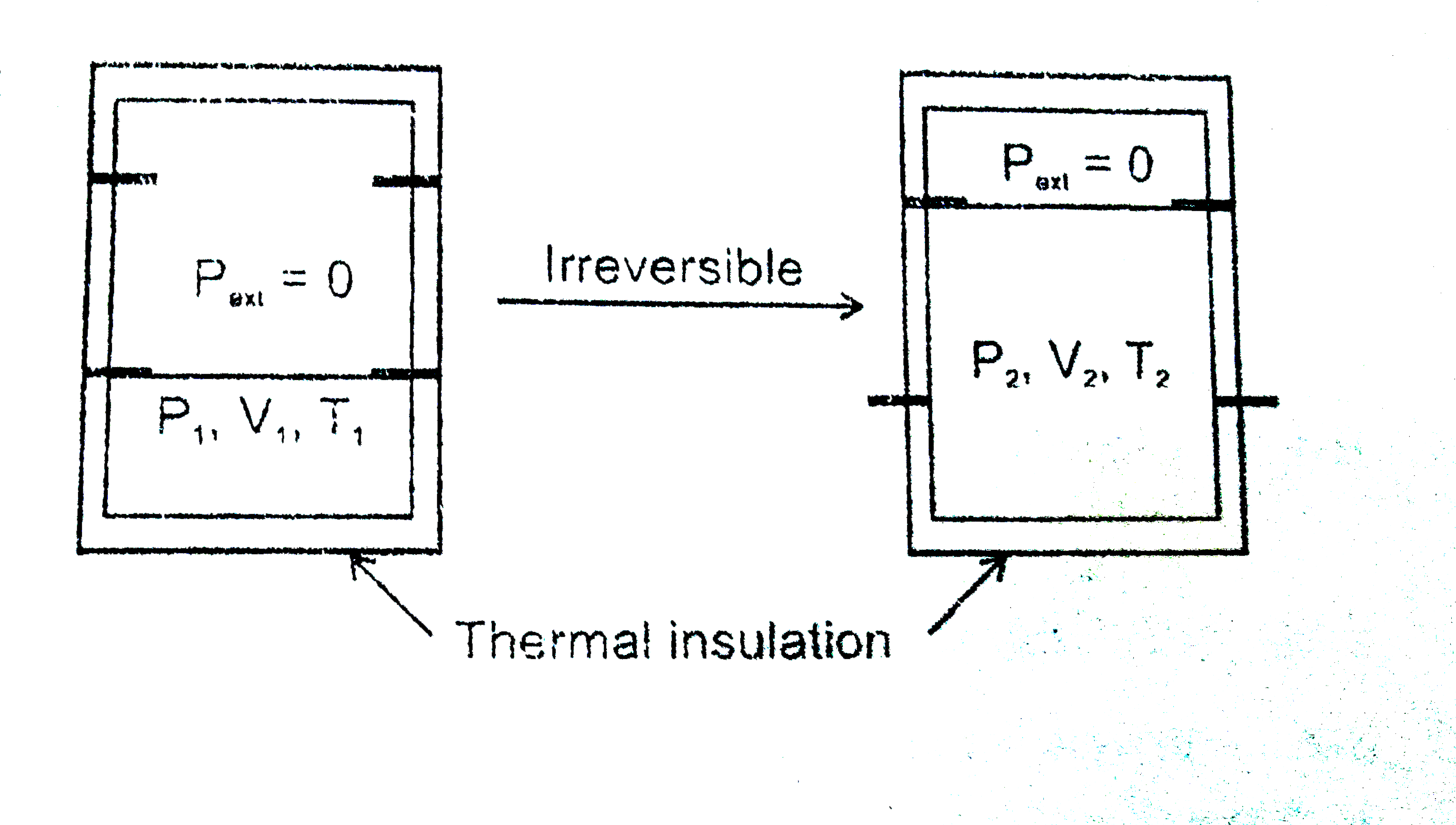
q=0
T2=T1
P2V2=PtV1
P2Vγ2=P1Vγ1
The correct Answer is:A, B, C
Since the vessel is thermally insulated so
q=0
pext=0, so w=0
so ΔU=0 (ideal gas)
Hence ΔT=0
⇒ΔT=0 ⇒T2=T1 ⇒P2V2=P1V1
The process is however adiabatic irriversible.
So we cannot applly P2Vγ2=P1V1
Hence ans is (A),(B),(C)
Topper's Solved these Questions
- THERMODYNAMICSBOOK - RESONANCECHAPTER - THERMODYNAMICSEXERCISE - Main
5 Videos
- THERMODYNAMICSBOOK - RESONANCECHAPTER - THERMODYNAMICSEXERCISE - Exercise-1 Part-I Subjective question
30 Videos
- THERMODYNAMICSBOOK - RESONANCECHAPTER - THERMODYNAMICSEXERCISE - Exercise-2 part -IV : Comprehension
11 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - CHEMISTRY
50 Videos
Similar Questions
A gas enclosed in a vessel has pressure P, volume V and absolute temperature T, write the formula for number of molecule N of the gas.
View SolutionTwo gases which are at pressure p1 volume V1 and temperature T1 and pressure p2 volume V2 and temperature T2, respectively are forced into a vessel of volume V at temperature T. Calculate pressure of the mixture.
View Solution
Knowledge Check
An ideal gas in thermally insulated vessel at internal (pressure)=P1,(volume)=V1 and absolute temperature=T1 expands irreversiby against zero external, pressure , as shown in the diagram,
The final internal pressure, volume and absolute temperature of the gas are p2,V2andT2, respectively . For this expansion
 Aq=0BT2=T1Cp2V2=p1V1DP2Vγ2=P1Vγ2
Aq=0BT2=T1Cp2V2=p1V1DP2Vγ2=P1Vγ2Two containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
AP1T1+P2T2BP1T1+P2T2(T1+T2)2CP1T2+P2T2(T1+T1)2DP12T1+P22T2Two containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
Ap1T2+p2T1T1×T2Bp1T2+p2T1T1+T2C12[p1T2+p2T1T1T2]Dp1T2−p2T1T1×T2]
A gas at constant pressure P1,volumeV1 and temperture T1 is suddenly compressed to V12 and then slowly expanded to V1 again.Find the final temperature and pressure.
View SolutionIf P, V and T stand for pressure, volume and absolute temperature of a gas, which of the following will be true for Boyle's Law
View SolutionTwo identical vessels contain the same gas at pressure P1 and P2 at absolute temperature T1andT2, respectively. On joining the vessels with a small tube as shown in the figure. The gas reaches a common temperature T and a common pressure P. Determine the ratio P/T

View SolutionOne mole of an ideal monoatomic gas at temperature T and volume 1 L expands to 2 L against a constant external pressure of one atm under adibatic conditions, then final temperature of gas will be :
View SolutionOne mole of an ideal monoatomic gas at temperature T and volume 1L expands to 2L against a constant external pressure of one atm under adiabatic conditions, then final temperature of gas will be:
View Solution