The ratio of $P$ to $V$ at any instant is constant and is equal to $1$ , for a monoatomic ideal gas under going a process. What is the molar heat capacity of the gas

$\frac{3 R}{2}$

$\frac{4 R}{2}$

$\frac{5 R}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

The ratio of P to V at any instant is constant and is equal to 1. for a monoatomic ideal gas undergoing a process. What is the molar heat capacity of the gas?
A $\frac{3 R}{2}$
B $\frac{4 R}{2}$
C $\frac{5 R}{2}$
D0
A monoatomic ideal gas undergoes a process $A B C$ . The heat given to the gas is

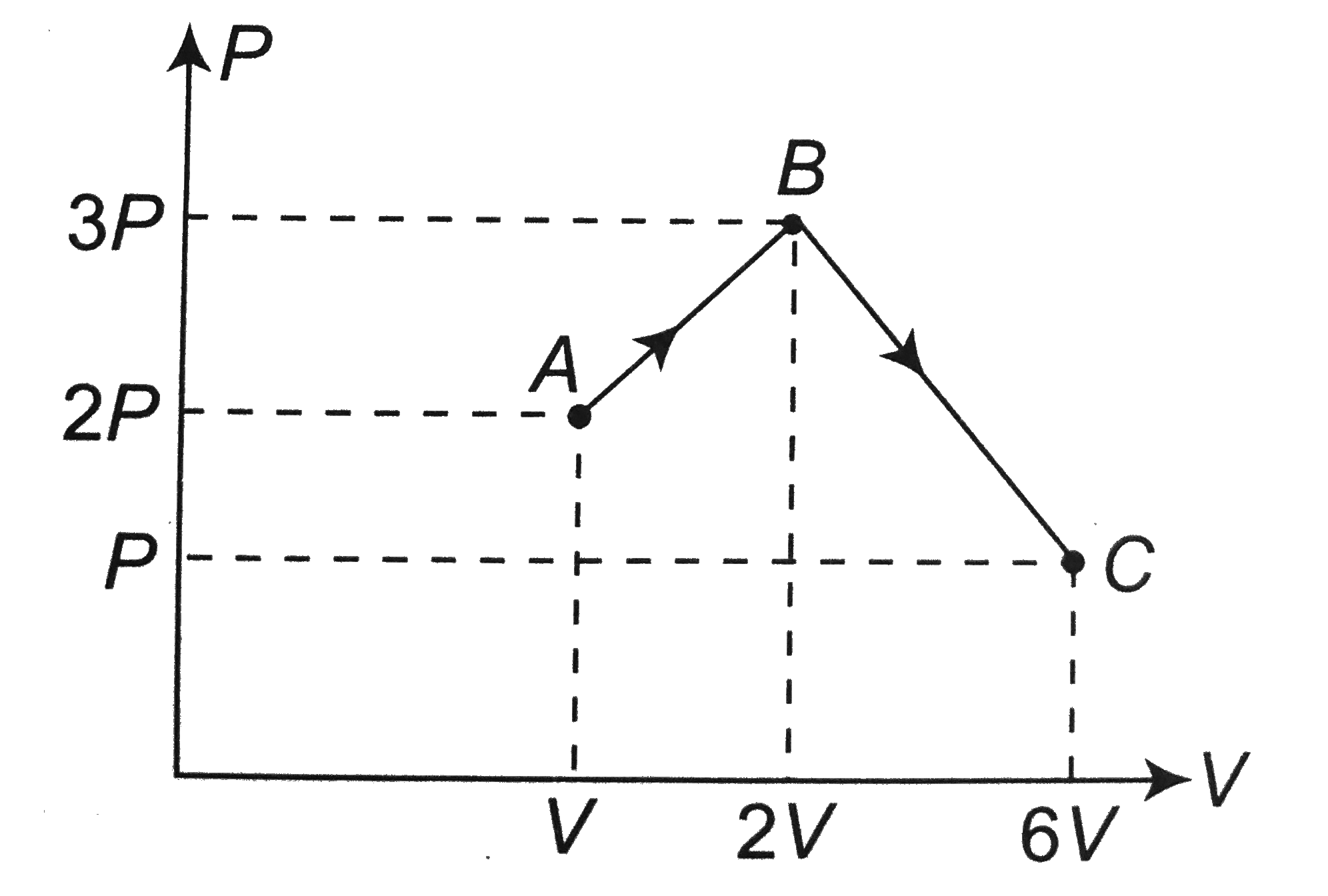A $7.5 P V$
B $12.5 P V$
C $16.5 P V$
D $20.5 P V$
The molar heat capacity of a gas in a process
Ais either $C_{V} or C_{P}$
Blies between $C_{V} or C_{P}$
Cmay range from zero to infinity
Dcan have any real value