Two identical vessels contain the same gas at pressure P1 and P2 at absolute temperature T1andT2, respectively. On joining the vessels with a small tube as shown in the figure. The gas reaches a common temperature T and a common pressure P. Determine the ratio P/T

[P1T1+P2T2T1T2]
12[P1T1+P2T2T1T2]
12[P1T2+P2T1T1T2]
[P1T2+P2T1T1T2]
The correct Answer is:C
On combining the two vessels the total number of moes remains constant , i.e.,n=n1+n2
Using gas equation, we can write , n1+P1VRT1,n2=P2VRT2
and n=P(2V)RT
where V is the volume of each vessel.
Thus P(2V)RT=P1VRT1+P2VRT2orPT=12[P1T1+P2T2] .
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:A2ZChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:First Law Of Thermodynamics , Internal Energy And Work Done
Explore 55 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:A2ZChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Application Of First Law Of Thermodynamics In Different Situations
Explore 25 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:A2ZChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Chapter Test
Explore 29 Videos
- GRAVITATIONBook:A2ZChapter:GRAVITATIONExercise:Chapter Test
Explore 29 Videos
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:Motion With Constant Acceleration
Explore 15 Videos
Similar Questions
Two vessels of volume (V1)and(V2) contain the same ideal gas. The pressures in the vessels are (P1)and(P2) and the temperatures are (T1)and(T2) respectively . The two vessels are now connected to each other through a narrow tube. Assuming thar no heat is exchanged between the surrounding and the vessels, find the common pressure and temperature attained after the connection.
View SolutionA gas can be liquefied at temperature T and pressure P provided
View Solution
Knowledge Check
Two containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
AP1T1+P2T2BP1T1+P2T2(T1+T2)2CP1T2+P2T2(T1+T1)2DP12T1+P22T2Two containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
Ap1T2+p2T1T1×T2Bp1T2+p2T1T1+T2C12[p1T2+p2T1T1T2]Dp1T2−p2T1T1×T2]A gas can be liquefied at temperature T and pressure P provided
AT=Tc and P<PCBT<Tc and P>PcCT>TC and P>PCDT>TC and P<PC
Two idential container joined by a small pipe initially contain the same gas at pressure p0 and absolute temperature T0. One container is now maintained at the same temperature while the other is heated to 2T0. The common pressure of the gas
View SolutionTwo identical containers joned by a small pipe initially contain the same gas at pressue po and abosolute temperature To. One container is now mantained at the same temperature while the other is heated to 2T0. The commmon pressure of the gases will be
View SolutionA given quantity of a ideal gas is at pressure P and absolute temperature T. The isothermal bulk modulus of the gas is
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
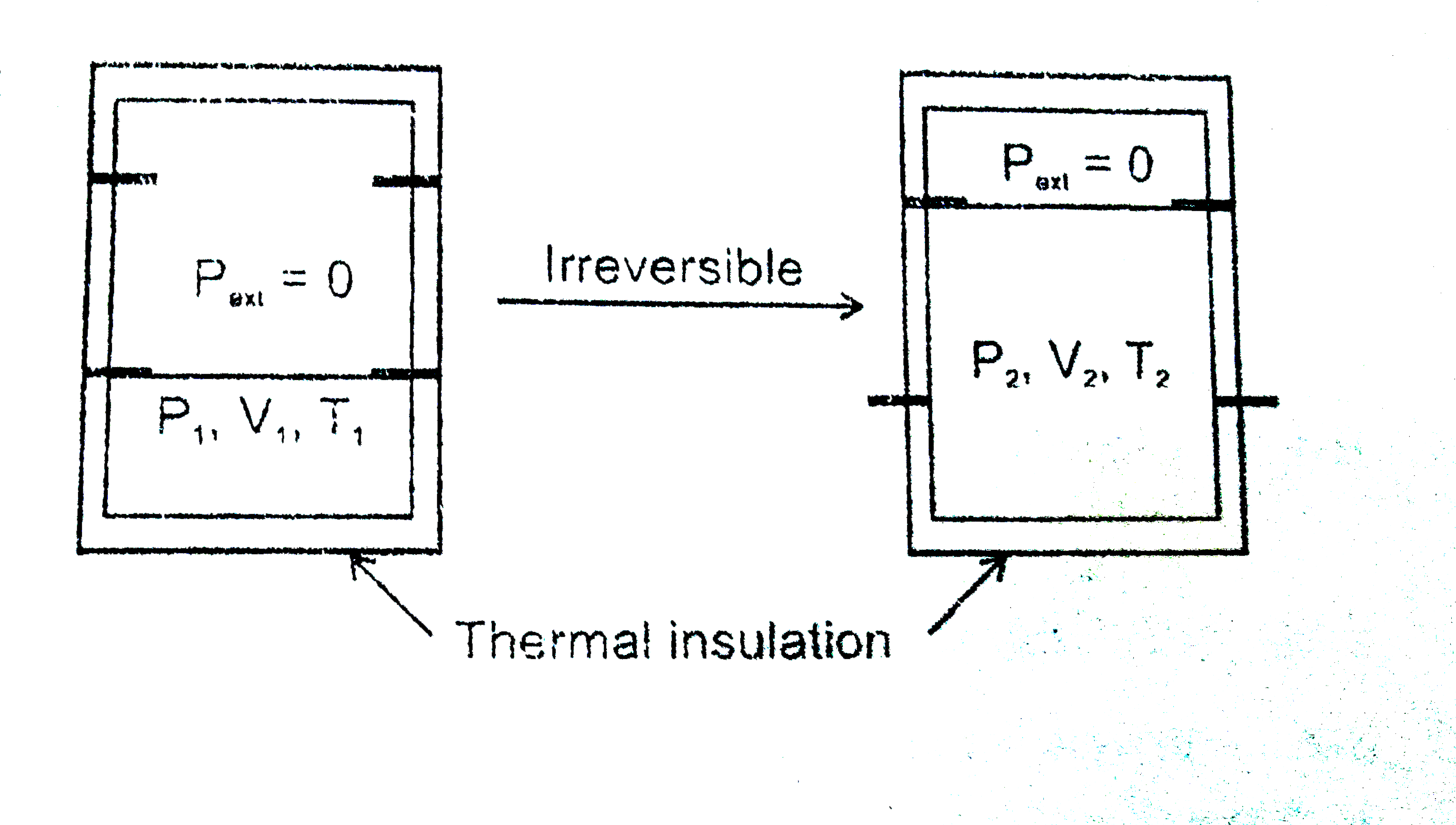
View SolutionA given quantity of a ideal gas is at pressure P and absolute temperature T. The isothermal bulk modulus of the gas is
View Solution

