An ideal gas in thermally insulated vessel at internal $(p r e s s u r e) = P_{1}, (v o l u m e) = V_{1}$ and absolute $t e m p e r a t u r e = T_{1}$ expands irreversiby against zero external, pressure , as shown in the diagram,
The final internal pressure, volume and absolute temperature of the gas are $p_{2}, V_{2} and T_{2}$ , respectively . For this expansion

$q = 0$

$T_{2} = T_{1}$

$p_{2} V_{2} = p_{1} V_{1}$

$P_{2} V_{2}^{γ} = P_{1} V_{2}^{γ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:a,b,c

Answer

Step by step video, text & image solution for An ideal gas in thermally insulated vessel at internal (pressure)=P_(1), (volume)=V_(1) and absolute temperature = T_(1) expands irreversiby against zero external, pressure , as shown in the diagram, The final internal pressure, volume and absolute temperature of the gas are p_(2), V_(2) and T_(2), respectively . For this expansion by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 CHEMISTRY THERMODYNAMICS AND THERMOCHEMISTRY

Topper's Solved these Questions

BOOK - IIT-JEE PREVIOUS YEAR (CHEMISTRY)CHAPTER - SURFACE CHEMISTRYEXERCISE - JEE Main And Advanced
17videos
SURFACE CHEMISTRY

Knowledge Check

Question 1 - Select One or More
An ideal gas in a thermally insulated vessel at internal pressure $= P_{1}$ , volume $= V_{1}$ and absolute temperature $= T_{1}$ expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are $P_{2}, V_{2}$ and $T_{2}$ respectively. For this expansion.

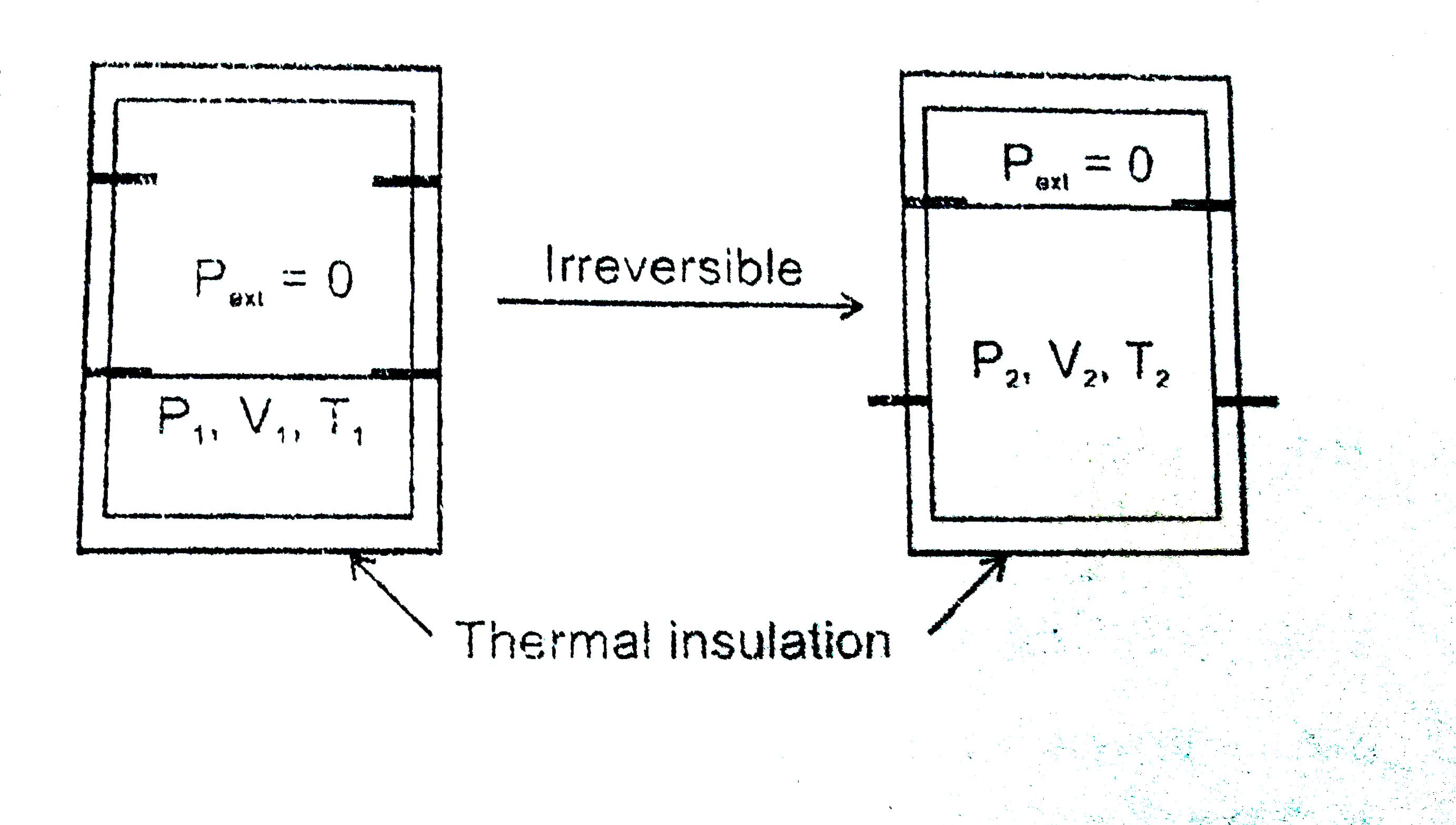A $q = 0$
B $T_{2} = T_{1}$
C $P_{2} V_{2} = P_{t} V_{1}$
D $P_{2} V_{2}^{γ} = P_{1} V_{1}^{γ}$
Question 2 - Select One
If P, V and T stand for pressure, volume and absolute temperature of a gas, which of the following will be true for Boyle's Law
A $V \propto T$ , when P is constant
B $V \propto \frac{1}{P}$ , when T is constant
C $P V = R T$
D $P V = n R T$
Question 3 - Select One
Two containers of equal volume contain the same gas at pressure $P_{1}$ and $P_{2}$ and absolute temperature $T_{1}$ and $T_{2}$ , respectively. On joining the vessels, the gas reaches a common pressure $P$ and common temperature $T$ . The ratio $P / T$ is equal to
A $\frac{p_{1} T_{2} + p_{2} T_{1}}{T_{1} \times T_{2}}$
B $\frac{p_{1} T_{2} + p_{2} T_{1}}{T_{1} + T_{2}}$
C $\frac{1}{2} [\frac{p_{1} T_{2} + p_{2} T_{1}}{T_{1} T_{2}}]$
D $\frac{p_{1} T_{2} - p_{2} T_{1}}{T_{1} \times T_{2}}]$

IIT-JEE PREVIOUS YEAR (CHEMISTRY)-THERMODYNAMICS AND THERMOCHEMISTRY-JEE Main And Advanced

Home
Ask Doubt
Profile

The correct Answer is:a,b,c

Topper's Solved these Questions

Similar Questions

Knowledge Check

If P, V and T stand for pressure, volume and absolute temperature of a gas, which of the following will be true for Boyle's Law

Two containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to

IIT-JEE PREVIOUS YEAR (CHEMISTRY)-THERMODYNAMICS AND THERMOCHEMISTRY-JEE Main And Advanced

Two containers of equal volume contain the same gas at pressure $P_{1}$ and $P_{2}$ and absolute temperature $T_{1}$ and $T_{2}$ , respectively. On joining the vessels, the gas reaches a common pressure $P$ and common temperature $T$ . The ratio $P / T$ is equal to