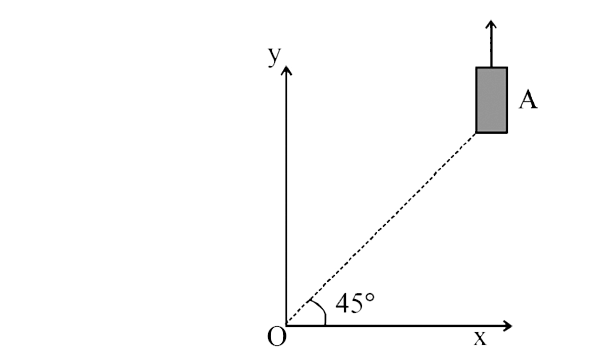
On a frictionless horizontal surface , assumed to be the plane , a small trolley is moving along a straight line parallel to the axis ( see figure) with a constant velocity of . At a particular instant , when the line makes an angle of with the axis , a ball is thrown along the surface from the origin . Its velocity makes an angle with the axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle made by the velocity vector of the ball with the axis in this frame .
(b) Find the speed of the ball with respect to the surface , if .
The correct Answer is:5
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:MCQ
Explore 2 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
Knowledge Check
A line makes an angle π4 with each y-axis and z-axis. The angle that it makes with the x - axis is
Aπ2Bπ4CπDπ6
A line makes an angle of 600 with each of X-axis and Y-axis. Find the acute angle made by the line with Z-axis.
View SolutionA line makes an angle of 600 with each of X-axis and Y-axis. Find the acute angle made by the line with Z-axis.
View SolutionA vector lying in x-y plane has a magnitude 3, and makes an angle 30∘ with the x-axis. Find its components along the two axes.
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
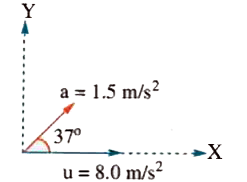
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionA mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin.
View SolutionFind the equation of the straight line which cuts off an intercept-5 from the y-axis and makes an angle of sin−1(1213) with the x-axis.
View SolutionA ball is thrown from the origin in the x-y plane with velocity 28.28m/s at an angle of 45∘ with x-axis.At the same instant a trolley also starts moving with uniform velocity of 10m/s along the positive x-axis . Initially , the trolley is located at 38m from the origin. Determine the time at which the ball hits the trolley.
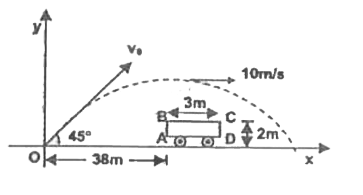
View Solution
