An object is kept fixed at the point and on a plank raised above the ground . At time the plank starts moving along the direction with an acceleration . At the same instant a stone is projected from the origin with a velocity as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle to the horizontal . All the motions are in the plane . Find and the time after which the stone hits the object . Take
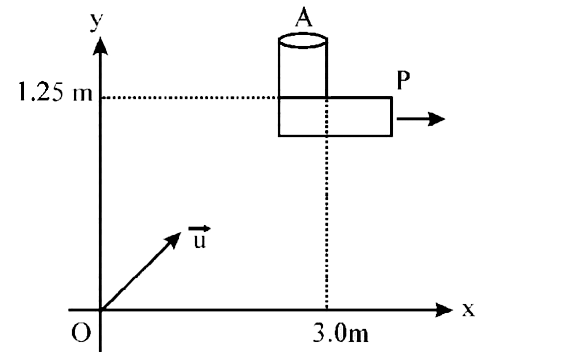
The correct Answer is:1s
Let after time ‘t’ the stone hits the object and be the angle which the velocity vector makes with horizontal
From question, we have following information Vertical displacement of stone is 1.25 m
Using
Therefore 1.25
Horizontal displacement of stone = 3 + displacement of object A.
Therefore
We have
Horizontal component of velocity (of stone) = vertical component (because velocity vector is inclined at with horizontal).
Therefore
The right-hand side is written because the stone is in its downward motion. Therefore
Multiplying equation (iii) with t can write.
Now doing (iv)-[(iii)+(i)]
It gives
Now, we can write 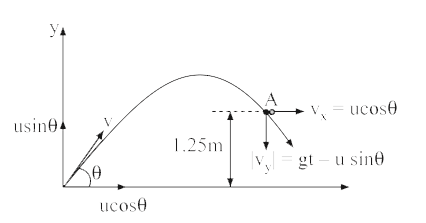
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:MCQ
Explore 2 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
A balloon starts rising from the ground with a constant acceleration of 1.25m/s2. After 8 s, a stone is released from the balloon. Find the time taken by the stone to reach the ground. (Take g=10m/s2)
View SolutionA balloon starts rising from the ground with an acceleration of 1.25 m/s2 . A stone is released from the balloon after 10s. Determine
(1) maximum height of ston from ground
(2) time taken by stone to reach the ground
View SolutionA balloon starts rising from ground from rest with an upward acceleration 2m/s2. Just after 1 s, a stone is dropped from it. The time taken by stone to strike the ground is nearly
View SolutionA stone is allowed to fall from the top of a tower 100m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25m/s. Calculate when and where the two stones will meet.
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
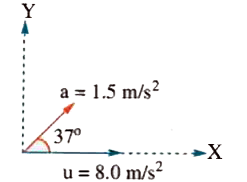
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionA stone is projected vertically up from the ground with velocity 40ms−1 . The interval of time between the two instants at which the stone is at a height of 60 m above the ground is (g=10ms−2)
View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

View SolutionA block is placed over a plank. The coefficient of friction between the block and the plank is μ=0.2. Initially both are at rest, suddenly the plank starts moving with acceleration a0=4m/s2. The displacement of the block in 1 is (g=10m/s2)
View SolutionTwo objects of masses 100g and 200g are moving along the same line in the same direction with velocities of 2m/s and 1m/s, respectively. They collide and after the collison, the first object moves at a velocity of 1.67m/s in the same direction. Determine the velocity of the second object.
View SolutionA stone is projected from point P on the inclined plane with velocity v0=10m/sec directed perpendicular to the plane. The time taken (in second) by the stone to strike the horizontal ground S is (Given PO=l=10meter)(Take g=10m/s2)

View Solution

