A large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .

The correct Answer is:(3.75ˆi+6.25gˆj)m/s
Let after time ‘t’ the stone hits the object and be the angle which the velocity vector makes with horizontal
From question, we have following information Vertical displacement of stone is 1.25 m
Using sy=uyt+12ayt2
Therefore 1.25 =(usinθ)t−12>2or(usinθ)t=1.25+5t2...(i)
Horizontal displacement of stone = 3 + displacement of object A.
Therefore (ucosθ)t=3+12at2
We have a=1.5m/s2,Hence (ucosθ)t=3+0.75t2.....(ii)
Horizontal component of velocity (of stone) = vertical component (because velocity vector is inclined at 45∘ with horizontal).
Therefore (ucosθ)=>−(usinθ)........(iii)
The right-hand side is written because the stone is in its downward motion. Therefore >>usinθ
Multiplying equation (iii) with t can write. (ucosθ)t+(usinθ)t=10t2......(iv)
Now doing (iv)-[(iii)+(i)]
It gives 4.25t2−4.25ort=1s Substituting t=1 s in (i) and (ii) we get
usinθ=6.25m/sorvy=6.25manducosθ=3.75m/sorux=3.75m/s
Now, we can write u=uxˆi+uyˆioru=(3.75ˆi+6.25ˆj)m/s 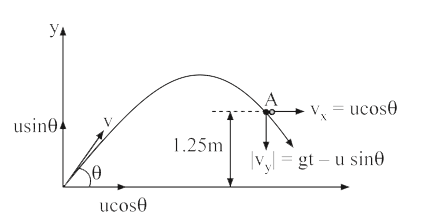
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:MCQ
Explore 2 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
Knowledge Check
in the question number 4, if the horizontal displacement of the particle as seen by an observer on the ground is zero, the speed of the box with respect to the ground at the instant when particle was projected is
AucosαBusinαcosθCucos(α+θ)cosθDusinθsinαcosθ
A particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle is projected along an inclined plane as shown in figure. What is the speed of the particle when it collides at point A ? (g=10ms2)

View SolutionA particle slides down on a smooth incline of inclination 30∘, fixed in an elevator going up with an acceleration 2m/s2. The box of incline has width 4m. The time taken by the particle to reach the bottom will be

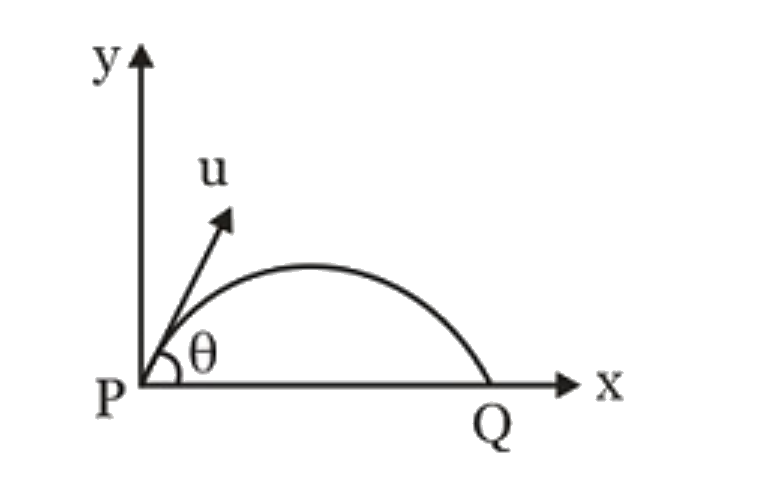
View SolutionA particle of mass m , initial speed u and angle of projection θ is projected as shown in the figure. Average torque on the projectile between initial and final positions P and Q about the point of projection is
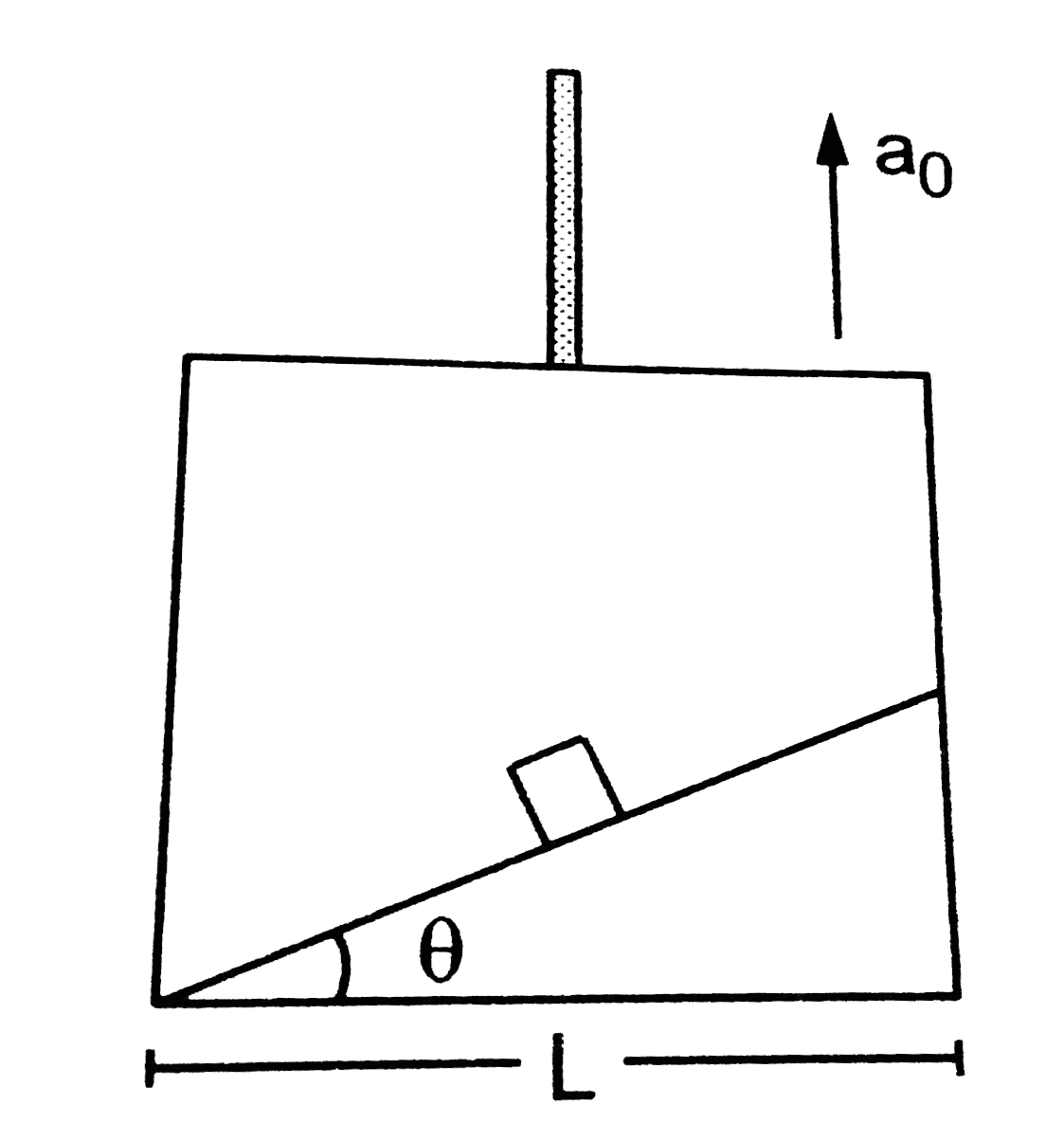
View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an accelerationa0. The base of the incline has a length L.Find the time taken by the particle to reach the bottom.
View SolutionA particle of mass m is projected from the ground with an initial speed u at an angle α. Find the magnitude of its angular momentum at the highest point of its trajector about the point of projection.
View Solution


 .
.