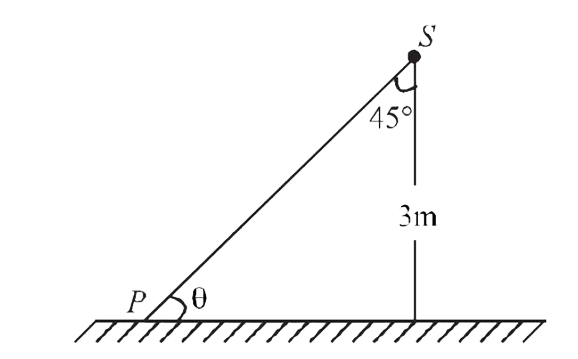
A spot light S rotates in a horizontal plane with a constant angular velocity of 0.1rad/s. The spot of light P move along the wall at a disatnce 3m. What is the velocity of the spot P when θ=45∘ ?
The correct Answer is:(u2)sin2θ)gcosθ
To solve the problem, we need to find the velocity of the spot of light P on the wall when the angle θ is 45∘. The spotlight rotates with a constant angular velocity ω=0.1rad/s and the distance from the spotlight to the wall is D=3m.
1. Understanding the Geometry:
The spotlight S rotates in a horizontal plane, and the light spot P moves along the wall at a distance D=3m. The angle θ is the angle between the line from the spotlight to the wall and the vertical line.
2. Finding the Radius r:
The radius r from the spotlight to the point P on the wall can be calculated using the formula:
r=Dcos(θ)
For θ=45∘:
r=3cos(45∘)=31√2=3√2m
3. Calculating the Linear Velocity v:
The linear velocity v of the spot of light P can be calculated using the formula:
v=ω⋅r⋅sin(θ)
Substituting the known values:
v=0.1rad/s⋅(3√2)⋅sin(45∘)
Since sin(45∘)=1√2:
v=0.1⋅(3√2)⋅1√2=0.1⋅3=0.3m/s
4. Final Calculation:
Therefore, the velocity of the spot P when θ=45∘ is:
v=0.3m/s
Final Answer:
The velocity of the spot P when θ=45∘ is 0.3m/s.
The spotlight S rotates in a horizontal plane, and the light spot P moves along the wall at a distance D=3m. The angle θ is the angle between the line from the spotlight to the wall and the vertical line.
The radius r from the spotlight to the point P on the wall can be calculated using the formula:
r=Dcos(θ)
For θ=45∘:
r=3cos(45∘)=31√2=3√2m
The linear velocity v of the spot of light P can be calculated using the formula:
v=ω⋅r⋅sin(θ)
Substituting the known values:
v=0.1rad/s⋅(3√2)⋅sin(45∘)
Since sin(45∘)=1√2:
v=0.1⋅(3√2)⋅1√2=0.1⋅3=0.3m/s
Therefore, the velocity of the spot P when θ=45∘ is:
v=0.3m/s
The velocity of the spot P when θ=45∘ is 0.3m/s.
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:MCQ
Explore 2 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
Spotlight S rotates in a horizontal plane with constant angular velocity of 0.1 rad/s The spot of light P moves along the wall at a distance of 3 m The velocity of the spot P when θ = 45 is m/s (see - fig. ) is ……….. m/s
View SolutionA wheel rotates with a constant angular velocity of 300 rpm. The angle through which the wheel rotates in 1 s is.
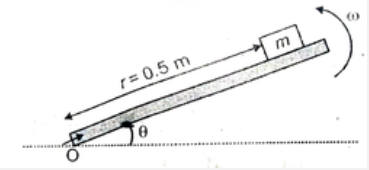
View SolutionA wooden plank OA rotates in vertical plane about horizontal axis through O with a constant angular velocity ω=3rad/s . As it passes the position θ=0 , a small mass m is placed upon it at a radial distance r=0⋅5 m . If the mass m starts sliding at θ=37∘ , find the coefficient of friction between mass and the plane .
View SolutionA rigid body is spinning about a fixed point (3,-2,-1) with an angular velocity of 4 rad/s, the axis of rotation being in the direction of (1,2,-2). Find the velocity of the particle at point (4,1,1).
View SolutionA rigid body is spinning about a fixed point (3,-2,-1) with an angular velocity of 4 rad/s, the axis of rotation being in the direction of (1,2,-2). Find the velocity of the particle at point (4,1,1).
View SolutionA ladder AP of length 5m inclined to a vertical wall is slipping over a horizontal surface with velocity of 2m/s, when A is at distance 3m from ground. What is the velocity of COM at this moment?

View SolutionCalculate the instantenous power of a wheel rotating with an angular velocity of 20rad/s, when a torque of 10Nm is applied to it.
View SolutionCalculate the instantenous power of a wheel rotating with an angular velocity of 20rad/s, when a torque of 10Nm is applied to it.
View SolutionA light ray is incident on a rotating mirror, which is rotating with angular speed 3rad/s as shown in figure. The speed of bright spot on the wall when θ=30∘

View SolutionA wheel is rotating with an angular velocity of 3rads−1. If the angular acceleration is 2rads−1 then calculate its angular velocity after 5 second.
View Solution

