A mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin.
is zero
Remains constant
Goes on increasing
Goes on decreasing
The correct Answer is:B
To solve the problem of determining the behavior of the angular momentum of a mass m moving with a constant velocity parallel to the x-axis away from the origin, we can follow these steps:
Step 1: Understand Angular Momentum
Angular momentum L with respect to a point (in this case, the origin) is defined as:
L=r×p
where r is the position vector from the origin to the mass, and p is the linear momentum of the mass, given by p=mv.
Step 2: Define the Position and Velocity
Let’s assume the mass m is moving along a line parallel to the x-axis at a constant height y=a (where a is a constant). The position vector r of the mass can be expressed as:
r=(x,a)
where x is the x-coordinate that changes over time as the mass moves away from the origin.
The velocity v of the mass is:
v=(vx,0)
where vx is a constant (the speed along the x-axis).
Step 3: Calculate the Angular Momentum
The angular momentum L can be calculated as:
L=r×p=r×(mv)
Substituting for r and p:
L=(x,a)×(mvx,0)
Step 4: Compute the Cross Product
The cross product in two dimensions can be calculated as:
L=m⋅vx⋅(x⋅0−a⋅1)=−m⋅vx⋅a
This shows that the angular momentum is:
L=−mavx
The negative sign indicates the direction of angular momentum, but the magnitude is what we are interested in.
Step 5: Analyze the Result
Since m, a, and vx are all constants (the mass, the constant height, and the constant velocity), the angular momentum L remains constant over time as the mass moves away from the origin.
Conclusion
Thus, the angular momentum of the mass with respect to the origin remains constant as it moves away with a constant velocity parallel to the x-axis.
Final Answer
The angular momentum remains constant.
---
Angular momentum L with respect to a point (in this case, the origin) is defined as:
L=r×p
where r is the position vector from the origin to the mass, and p is the linear momentum of the mass, given by p=mv.
Let’s assume the mass m is moving along a line parallel to the x-axis at a constant height y=a (where a is a constant). The position vector r of the mass can be expressed as:
r=(x,a)
where x is the x-coordinate that changes over time as the mass moves away from the origin.
v=(vx,0)
where vx is a constant (the speed along the x-axis).
The angular momentum L can be calculated as:
L=r×p=r×(mv)
Substituting for r and p:
L=(x,a)×(mvx,0)
The cross product in two dimensions can be calculated as:
L=m⋅vx⋅(x⋅0−a⋅1)=−m⋅vx⋅a
This shows that the angular momentum is:
L=−mavx
The negative sign indicates the direction of angular momentum, but the magnitude is what we are interested in.
Since m, a, and vx are all constants (the mass, the constant height, and the constant velocity), the angular momentum L remains constant over time as the mass moves away from the origin.
Thus, the angular momentum of the mass with respect to the origin remains constant as it moves away with a constant velocity parallel to the x-axis.
The angular momentum remains constant.
Similar Questions
A body of mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Calculate its angular momentum with respect to the origin?
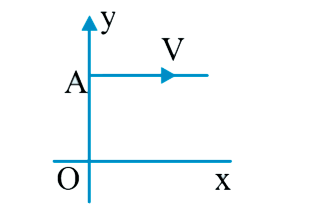
View SolutionIf the particle of mass m is moving with constant velocity v parallel to x-axis in x-y plane as shown in (figure), Find its angular momentum with respect of origin at any time t.
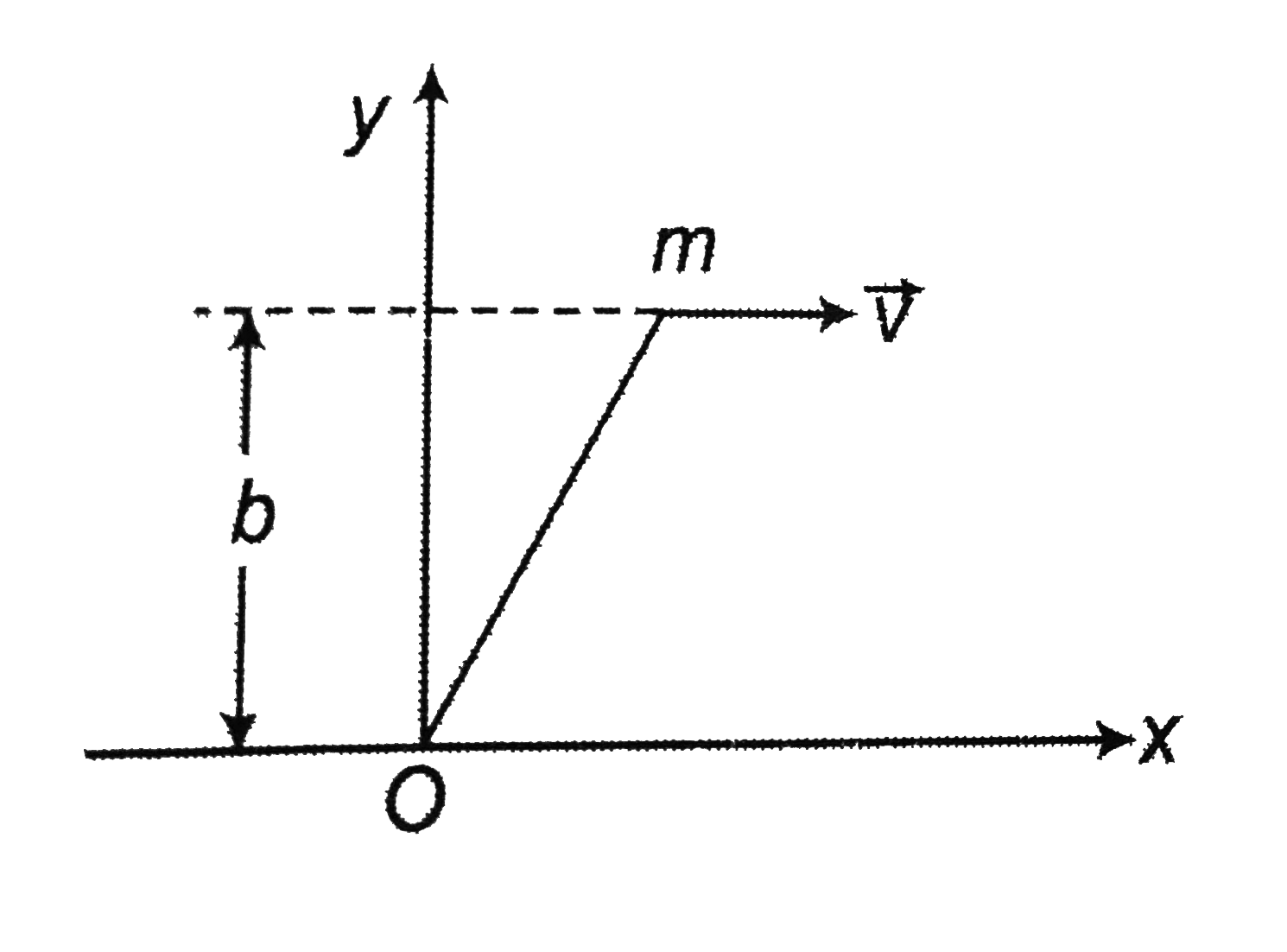
View Solution
Knowledge Check
A mass M moving with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
Aa. is zeroBb. remains constantCc. goes on increasingDd. goes on decreasing
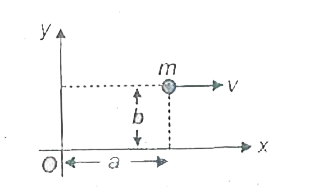
A particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is
View SolutionA particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
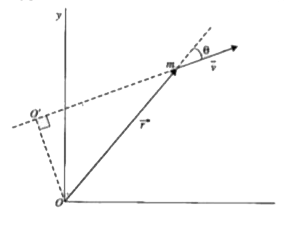
View SolutionA particle of mass m moves in the XY plane with constant velocity v along the straight line PQ as shown in the figure. Its angular momentum with respect to origin O is(θ is angle between→v and x-axis)

View SolutionFind the equation of a line parallel to x-axis and passing through the origin.
View SolutionFind the equation of a line parallel to x-axis and passing through the origin.
View SolutionA solid sphere is rotating with a constant angular velocity about an axis touching the surface. Its angular momentum will be:
View SolutionA point mass 10 g moves in the xy plane with a velocity 2ms−1 along a straight line. Find the magnitude and direction of its angular momentum (i) with respect to the origin O and (ii) with respect to the origin O. The magnitude of the position vector →r is 0.5 m and the angle θ=30∘.
View Solution

