A body of mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Calculate its angular momentum with respect to the origin?
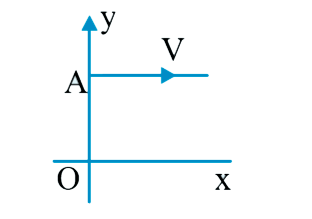
L=mvr⊥ L=mv(OA) as OA and v are both contant, the angular momentum remains constant.
Similar Questions
A particle performs uniform circular velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin.
View SolutionIf the particle of mass m is moving with constant velocity v parallel to x-axis in x-y plane as shown in (figure), Find its angular momentum with respect of origin at any time t.

View Solution
Knowledge Check
A body of mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin
Ais zeroBremains constantCgoes on increasingDgoes on decreasingA mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin.
AzeroBremains constantCgoes on increasingDgoes on decreasingA mass m moving with a constant velocity along a line parallel to the axis, away from the origin. Its anguarl momentum with respect to the origin
Ais zeroBremains constantsCgoes on increasingDgoes on decreasing
A particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
View SolutionA particle is moving in the xy-plane with a constant velocity along a line parallel to the X-axis away from the origin. The magnitude of its angular momentum about the origin.
View SolutionA particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is

View SolutionIf a particle of mass m is moving with constant velocity v parallel to x-axis in x−y plane as shown in fig. Its angular moment with respect to origin at any time t will be
View SolutionA mass M moving with a constant velocity parlale to the X-axis. Its angular momentum with respect to the origin
View Solution
