Question

A mass M moving with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin

Options

A. a. is zero
B. b. remains constant
C. c. goes on increasing
D. d. goes on decreasing

Answer

b

Explanation

To find the angular momentum of a mass $$M$$ moving with a constant velocity $$v$$ parallel to the X-axis with respect to the origin, we can follow these steps:

Step 1: Understand the Setup
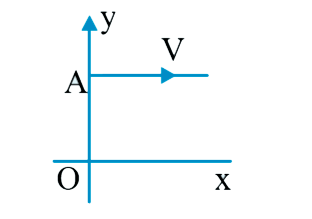
Consider a mass \( M \) moving along the X-axis at a constant velocity \( v \). Let's denote the position of the mass at any time \( t \) as \( (x, 0) \), where \( x = vt \). The distance from the origin to the mass is given by \( r = x \).

Step 2: Define the Angular Momentum
The angular momentum \( L \) of a particle with respect to a point (in this case, the origin) is given by the formula:
\( L = r \times p \)
where \( p \) is the linear momentum of the mass, defined as:
\( p = M \cdot v \)

Step 3: Calculate the Perpendicular Distance
The angular momentum can also be expressed in terms of the perpendicular distance from the line of motion to the point about which we are calculating the angular momentum. Since the mass is moving parallel to the X-axis, the perpendicular distance \( r_{\perpendicular} \) from the origin to the line of motion is simply the Y-coordinate of the mass, which is \( 0 \) in this case. However, if we consider the mass to be at a distance \( r_1 \) from the origin, we can express the perpendicular distance as:
\( r_{\perpendicular} = r_1 \sin(\theta) \)
where \( \theta \) is the angle between the position vector and the velocity vector.

Step 4: Express Angular Momentum
Substituting the values into the angular momentum formula, we have:
\( L = M \cdot v \cdot r_{\perpendicular} \)
Since the perpendicular distance remains constant as the mass moves along the X-axis, we can conclude that:
\( L = M \cdot v \cdot r_1 \sin(\theta) \)

Step 5: Conclusion
Since both the mass \( M \) and the velocity \( v \) are constant, and the perpendicular distance does not change as the mass moves, the angular momentum \( L \) remains constant with respect to the origin. Therefore, the angular momentum of the mass \( M \) moving with a constant velocity parallel to the X-axis is constant.

Final Answer
The angular momentum \( L \) with respect to the origin is constant.

---