Consider a particle of mass m having linear momentum →p at position →r relative to the origin O. Let →L be the angular momentum of the particle with respect to the origin. Which of the following equations correctly relate(s) →r, →p and →L?
d→Ldt+→r×d→pdt=0
d→Ldt+d→rdt×→p=0
d→Ldt−d→rdt×→p=0
d→Ldt−→r×d→pdt=0
The correct Answer is:d
To find the relationship between the position vector →r, linear momentum →p, and angular momentum →L of a particle, we can follow these steps:
Step 1: Define Angular Momentum
The angular momentum →L of a particle with respect to the origin is defined as:
→L=→r×→p
where →r is the position vector of the particle and →p is the linear momentum of the particle.
Step 2: Express Linear Momentum
The linear momentum →p of a particle is given by:
→p=m→v
where m is the mass of the particle and →v is its velocity.
Step 3: Differentiate Angular Momentum
To find the relationship involving time, we differentiate the angular momentum →L with respect to time t:
d→Ldt=ddt(→r×→p)
Using the product rule for differentiation, we have:
d→Ldt=d→rdt×→p+→r×d→pdt
Step 4: Substitute Velocity
Since d→rdt is the velocity →v, we can rewrite the equation as:
d→Ldt=→v×→p+→r×d→pdt
Step 5: Analyze the Terms
Now, substituting →p=m→v into the equation:
→v×→p=→v×(m→v)
Since the cross product of a vector with itself is zero:
→v×→v=0
Thus, the equation simplifies to:
d→Ldt=0+→r×d→pdt
This leads to:
d→Ldt=→r×d→pdt
Step 6: Final Relation
We can rearrange this to express the relationship between →L, →r, and →p:
d→Ldt−→r×d→pdt=0
Conclusion
This final equation shows the relationship between the angular momentum →L, position vector →r, and the change in linear momentum d→pdt.
The angular momentum →L of a particle with respect to the origin is defined as:
→L=→r×→p
where →r is the position vector of the particle and →p is the linear momentum of the particle.
The linear momentum →p of a particle is given by:
→p=m→v
where m is the mass of the particle and →v is its velocity.
To find the relationship involving time, we differentiate the angular momentum →L with respect to time t:
d→Ldt=ddt(→r×→p)
Using the product rule for differentiation, we have:
d→Ldt=d→rdt×→p+→r×d→pdt
Since d→rdt is the velocity →v, we can rewrite the equation as:
d→Ldt=→v×→p+→r×d→pdt
Now, substituting →p=m→v into the equation:
→v×→p=→v×(m→v)
Since the cross product of a vector with itself is zero:
→v×→v=0
Thus, the equation simplifies to:
d→Ldt=0+→r×d→pdt
This leads to:
d→Ldt=→r×d→pdt
We can rearrange this to express the relationship between →L, →r, and →p:
d→Ldt−→r×d→pdt=0
This final equation shows the relationship between the angular momentum →L, position vector →r, and the change in linear momentum d→pdt.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:EQUILIBRIUM OF A RIGID BODY
Explore 13 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:MOMENT OF INERTIA
Explore 7 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTPS ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:MOTION OF CENTRE OF MASS
Explore 10 Videos
- PRACTICE PAPERSBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPERSExercise:All Questions
Explore 150 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTPS ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
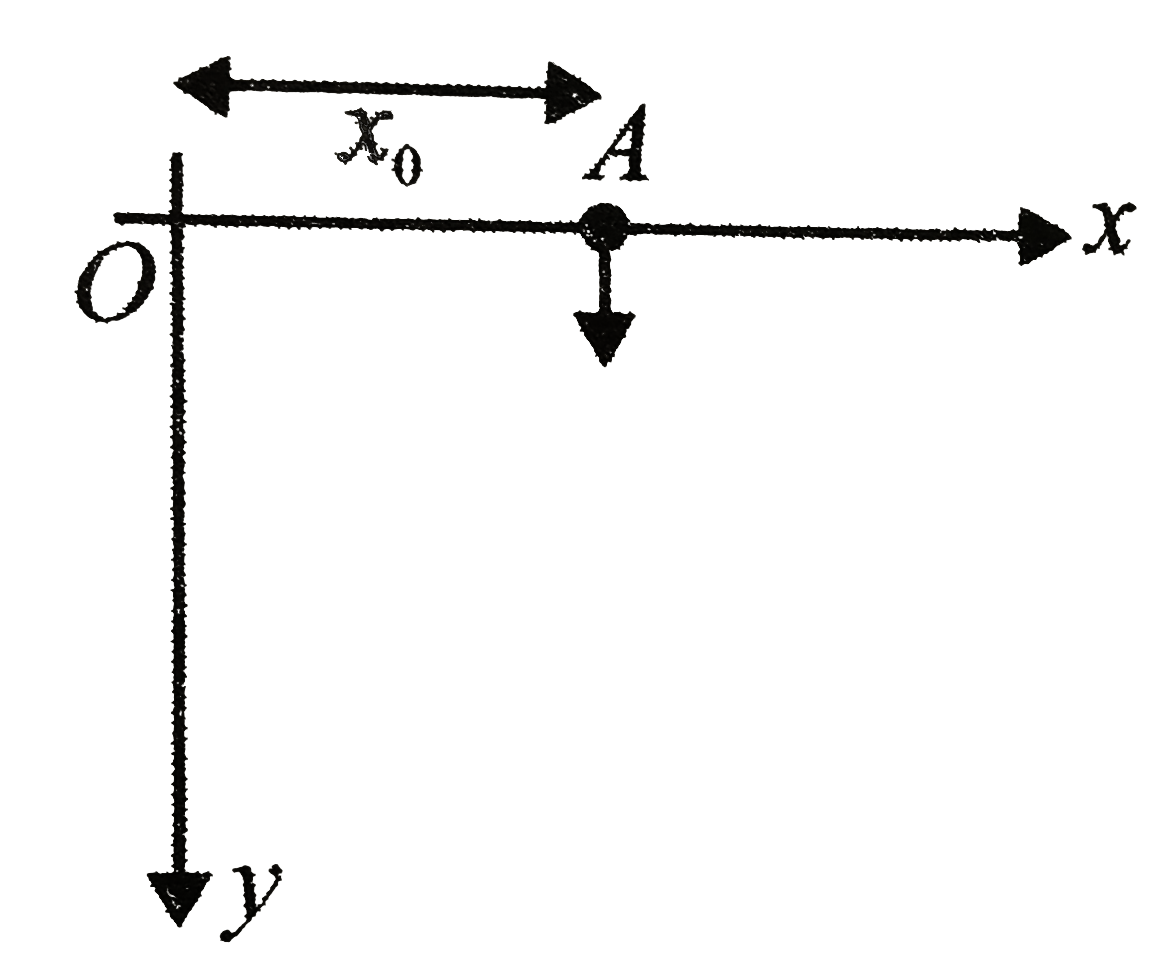
A particle of mass m is released from rest at point A in Fig., falling parallel to the (vertical) y-axis. Find the angular momentum of the particle at any time t with respect to the same origin O.
View SolutionIf a moving particle have linear momentum ¯¯¯P and position vector ¯r then choose the correct relation between ¯r,¯p and angular momentum ¯¯¯L of particle about the origin.
View Solution
Knowledge Check
For a moving particle (mass m, velocity v) having a momentum p, which one of the following correctly describes the kinetic energy of the particle?
Ap22mBp2mCv22mDv2m
A particle has a linear momentum p and position vector r. the angular momentum of this particle about the origin will not be zero under the conditions
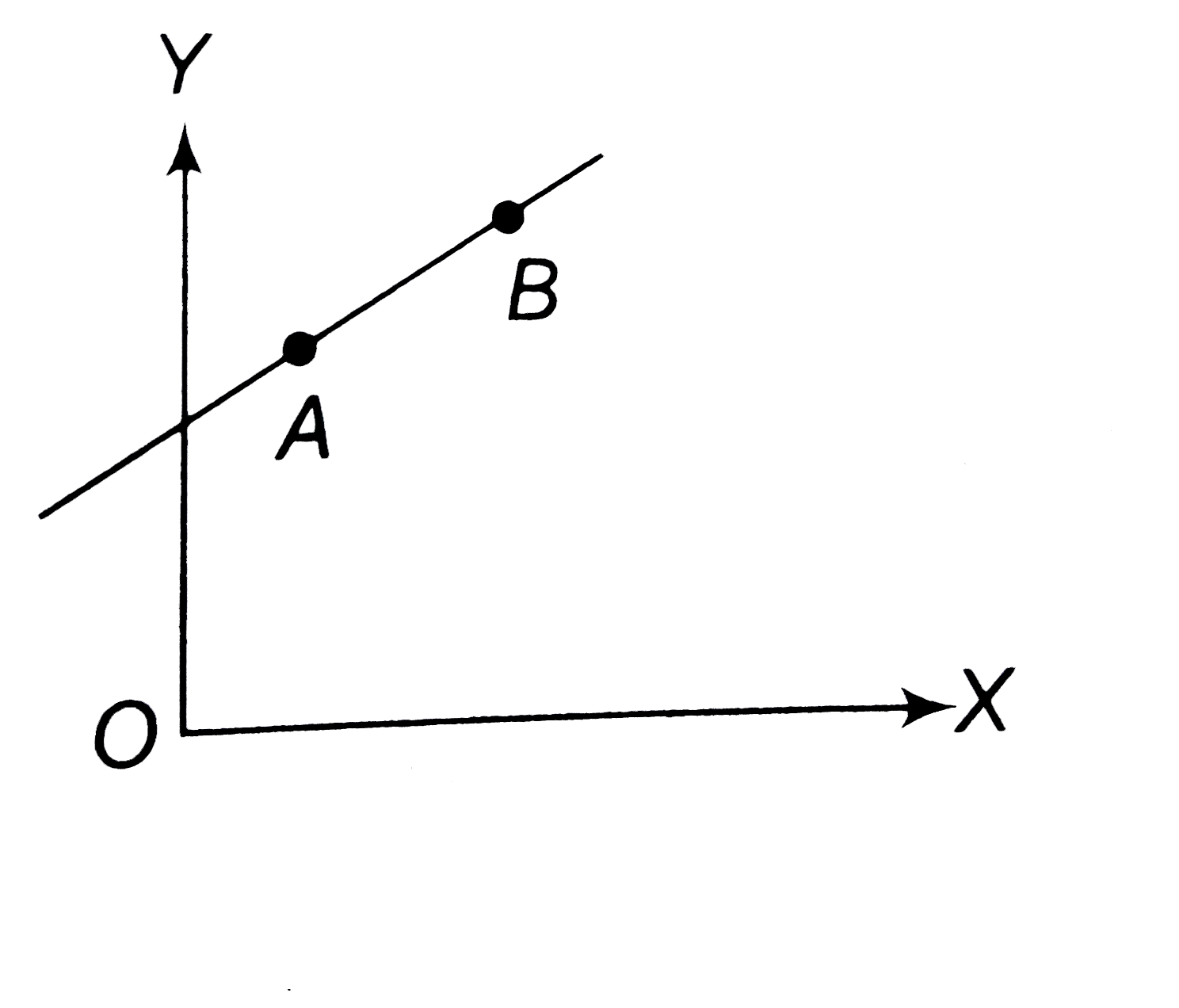
View SolutionA particle of mass m moves in the XY plane with a velocity v along the straight line AB. If the angular momentum of the particle with respect to origin O is LA when it is at A and LB when it is at B, then
View SolutionThe linear momentum of a particle varies with time as p=a0+at+bt2. Which of the following graph represents force and time relation ?
View SolutionA particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
View SolutionA charged particle of mass m and charge q is released from rest the position (x0,0) in a uniform electric field E0ˆj. The angular momentum of the particle about origin.
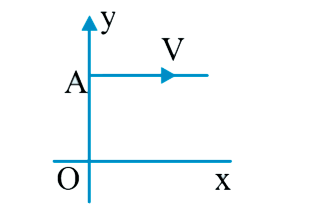
View SolutionA body of mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Calculate its angular momentum with respect to the origin?
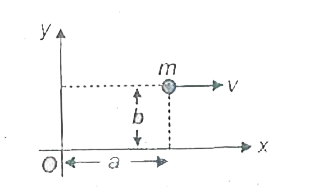
View SolutionA particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is
View Solution

