A disc is rotating with angular velocity ω. A force F acts at a point whose position vector with respect to the axis of rotation is r. The power associated with torque due to the force is given by
(→r×→F).→ω
(→r×→F)×→ω
→r.(→F×→ω)
→r×(→F.→ω)
The correct Answer is:a
To solve the problem, we need to find the power associated with the torque due to the force acting on a rotating disc. Let's break this down step by step.
Step 1: Understand the relationship between torque and force
Torque (τ) is defined as the cross product of the position vector (r) and the force vector (F). Mathematically, this is expressed as:
τ=r×F
Step 2: Relate power to torque
Power (P) associated with torque can be expressed as:
P=τ⋅ω
where ω is the angular velocity of the disc.
Step 3: Substitute the expression for torque
Substituting the expression for torque into the power equation, we have:
P=(r×F)⋅ω
Step 4: Simplify the expression
The expression (r×F)⋅ω represents the power associated with the torque due to the force acting on the disc. This is the final expression for power in terms of torque and angular velocity.
Conclusion
Therefore, the power associated with the torque due to the force acting on the rotating disc is given by:
P=(r×F)⋅ω
Torque (τ) is defined as the cross product of the position vector (r) and the force vector (F). Mathematically, this is expressed as:
τ=r×F
Power (P) associated with torque can be expressed as:
P=τ⋅ω
where ω is the angular velocity of the disc.
Substituting the expression for torque into the power equation, we have:
P=(r×F)⋅ω
The expression (r×F)⋅ω represents the power associated with the torque due to the force acting on the disc. This is the final expression for power in terms of torque and angular velocity.
Therefore, the power associated with the torque due to the force acting on the rotating disc is given by:
P=(r×F)⋅ω
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - EQUILIBRIUM OF A RIGID BODY
13 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - MOMENT OF INERTIA
7 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - MOTION OF CENTRE OF MASS
10 Videos
- PRACTICE PAPERSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions
150 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
Similar Questions
A disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.

View SolutionA body rotating with angular velocity ω stops after rotating for 2 sec. The torque necessary for this is?
View SolutionA circular disc is rotating about its own axis at an angular velocity ω. If P is exact midpoint of dise between axis and rim of disc then angular velocity of Pis
View SolutionA metal rod length l rotates about on end with a uniform angular velocity ω. A uniform magnetic field →B exists in the direction of the axis of rotation. Calculate the emf induced between the ends of the rod. Neglect the centripetal force acting on the free electrons as they moving in circular paths.
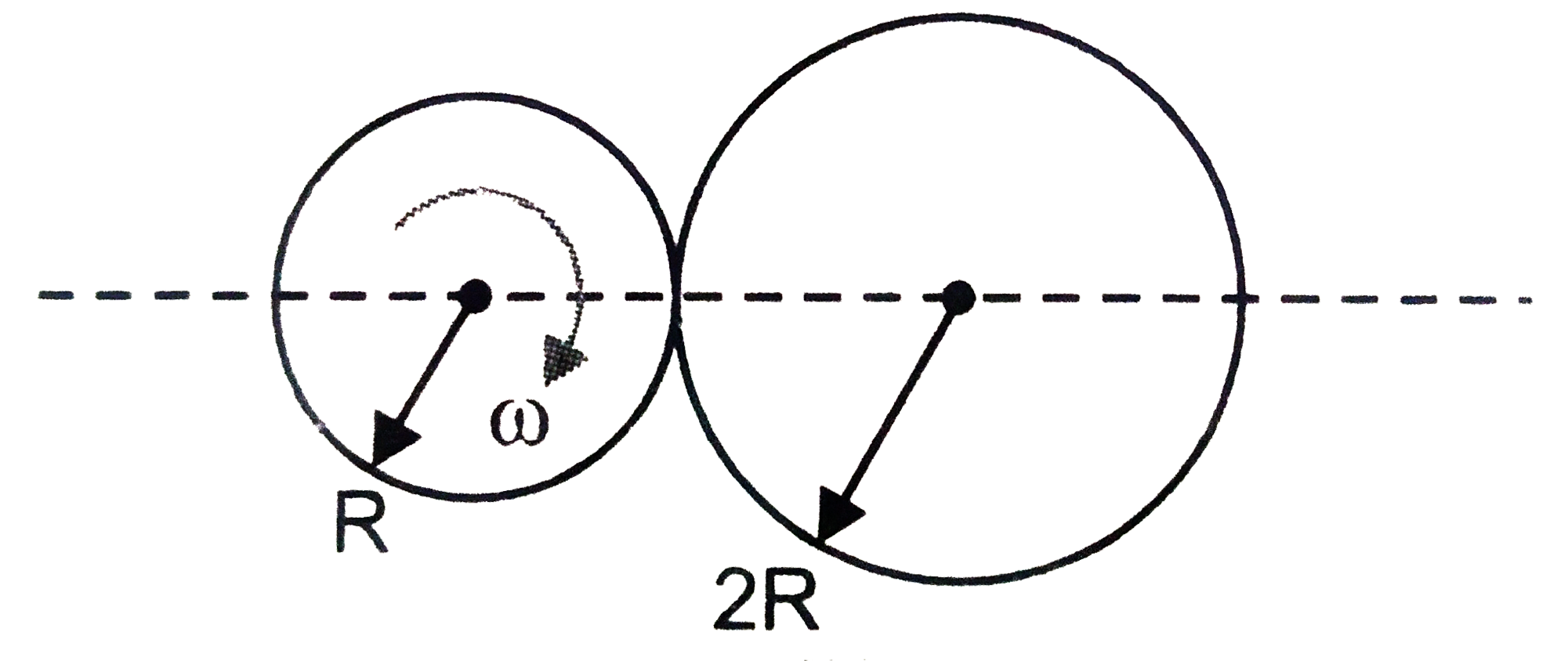
View SolutionTwo discs of radii Rand2R are pressed against each other. Initially, disc with radius R is rotating with angular velocity ω and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertia of smaller disc is I and of bigger disc is 2I about their respective axis of rotation. Find the angular velocity of bigger disc after long time.
View SolutionTwo discs of same moment of inertia rotating their regular axis passing through centre and perpendicular to the plane of disc with angular velocities ω1 and ω2. They are brought into contact face to the face coinciding the axis of rotation. The expression for loss of enregy during this process is :
View SolutionTwo discs of same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of disc with angular velocities ω1 and ω2. They are brought into contact face to face coinciding the axis of rotation. The expression for loss of energy during this process is
View SolutionThe force 7ˆi+3ˆj−5ˆk acts on a particle whose position vector is ˆi−ˆj+ˆk. What is the torque of a given force about the origin ?
View SolutionA force →F=4ˆi−10ˆj acts on a body at a point having position vector −5ˆi−3ˆj relative to origin of co-ordinates on the axis of rotation. The torque acting on the body is
View Solution
