A point mass 10 g moves in the xy plane with a velocity 2ms−1 along a straight line. Find the magnitude and direction of its angular momentum (i) with respect to the origin O and (ii) with respect to the origin O. The magnitude of the position vector →r is 0.5 m and the angle θ=30∘.
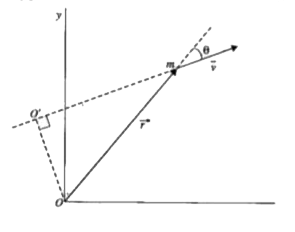
m=10g=0.010kg
v=2ms−1,r=−0.5m
OO. =rsinθ
=0.5sin30
=0.25 m
Angular momentum about O
=mvrsinθ
=0.01×2×0.25
=5×10−3J.s.
Angular momentum about O. = 0, because the direction of the velocity passes through O..
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
Explore 11 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (LONG ANSWER QUESTIONS)
Explore 8 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
A particle of mass m moves in the XY plane with constant velocity v along the straight line PQ as shown in the figure. Its angular momentum with respect to origin O is(θ is angle between→v and x-axis)

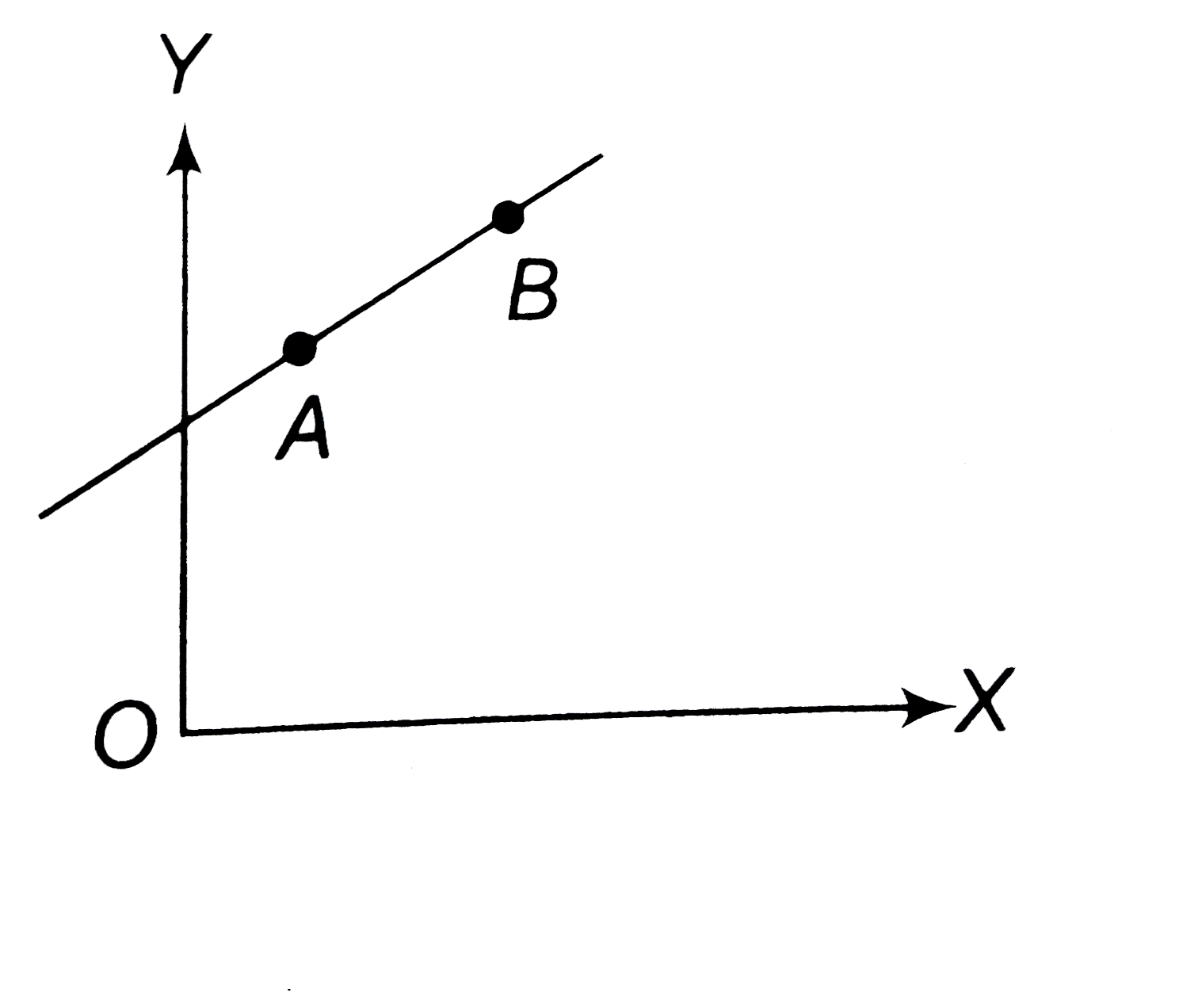
View SolutionA particle of mass m moves in the XY plane with a velocity v along the straight line AB. If the angular momentum of the particle with respect to origin O is LA when it is at A and LB when it is at B, then
View Solution
Knowledge Check
A mass M moving with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
Aa. is zeroBb. remains constantCc. goes on increasingDd. goes on decreasing
A mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin.
View SolutionA particle moves in xy-plane from position (1m,2m) to (3m,4m) in 2s. Find the magnitude and direction of average velocity.
View SolutionA body of mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Calculate its angular momentum with respect to the origin?
View SolutionA particle m starts with zero velocity along a line y=4d. The position of particle m varies as x=Asinωt, At ωt=π/2, its angular momentum with respect to the origin
View SolutionA particle of mass 300 g is moving with a speed of 20 ms−1 along the straight line y = x - 4√2. The angular momentum of the particle about the origin is (where y & x are in metres)
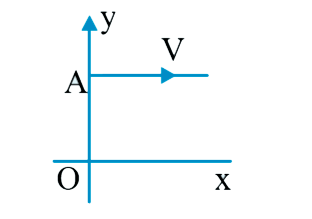
View SolutionIf the particle of mass m is moving with constant velocity v parallel to x-axis in x-y plane as shown in (figure), Find its angular momentum with respect of origin at any time t.

View SolutionA particle of mass m=3kg moves along a straight line 4y−3x=2 where x and y are in metre, with constant velocity v=5ms−1 the magnitude of angular momentum about the origin is
View Solution

