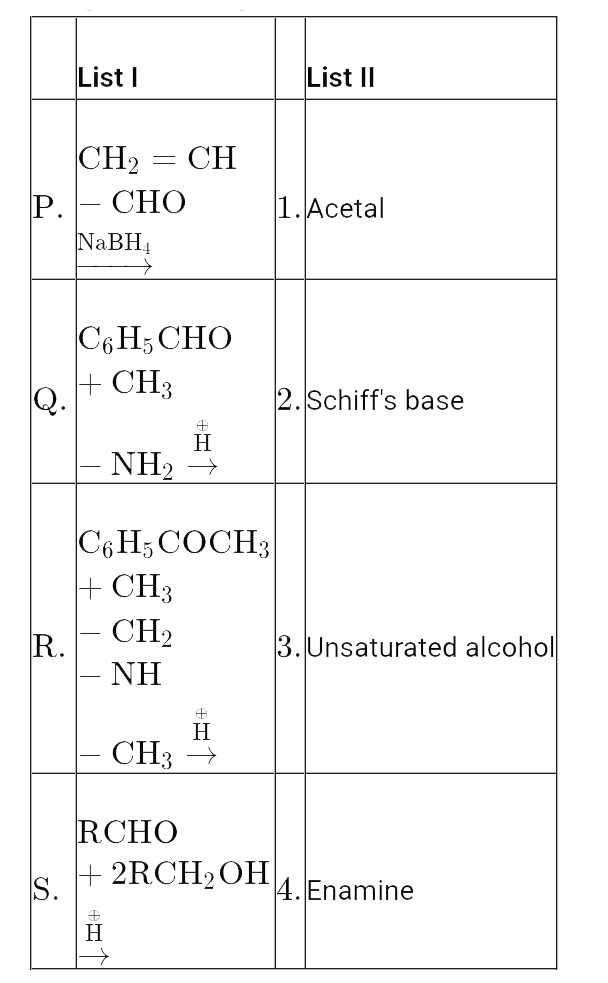
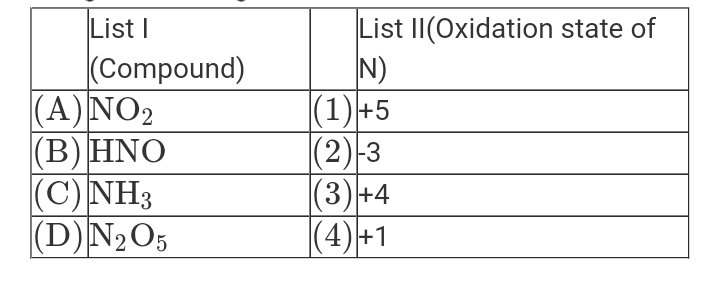
Match List I with List II and select the correct answer using the codes given below the lists.
The correct Answer is:B
To solve the problem of matching the physical quantities in List I with their corresponding dimensions in List II, we will derive the dimensional formulas for each physical quantity step by step.
Step 1: Angular Momentum
- Definition: Angular momentum (L) is given by the formula L=M⋅V⋅R, where M is mass, V is velocity, and R is the radius (or distance).
- Dimensional Formula:
- Mass (M) has the dimension (M).
- Velocity (V) has the dimension (LT^{-1}).
- Radius (R) has the dimension (L).
Therefore, the dimensional formula for angular momentum is:
(L)=(M)⋅(LT−1)⋅(L)=(ML2T−1)
Conclusion: Angular momentum corresponds to (3) ML²T⁻¹.
Step 2: Torque
- Definition: Torque (τ) is defined as the product of force and the distance from the pivot point, τ=F⋅R.
- Dimensional Formula:
- Force (F) has the dimension (MLT^{-2}).
- Distance (R) has the dimension (L).
Therefore, the dimensional formula for torque is:
(τ)=(F)⋅(L)=(MLT−2)⋅(L)=(ML2T−2)
Conclusion: Torque corresponds to (4) ML²T⁻².
Step 3: Surface Tension
- Definition: Surface tension (γ) is defined as force per unit length.
- Dimensional Formula:
- Force (F) has the dimension (MLT^{-2}).
- Length (L) has the dimension (L).
Therefore, the dimensional formula for surface tension is:
(γ)=(F)(L)=(MLT−2)(L)=(MT−2)
Conclusion: Surface tension corresponds to (2) MT⁻².
Step 4: Coefficient of Viscosity
- Definition: The coefficient of viscosity (η) is defined as the ratio of shear stress to shear rate.
- Dimensional Formula:
- Shear stress has the dimension (MLT^{-2}) (force per unit area).
- Shear rate has the dimension (LT^{-1}).
Therefore, the dimensional formula for the coefficient of viscosity is:
(η)=(F/A)(V/L)=(MLT−2)(L2)⋅(LT−1)=(MLT−2)(L2)⋅(L)=(ML−1T−1)
Conclusion: Coefficient of viscosity corresponds to (1) ML⁻¹T⁻¹.
Final Matching:
- A. Angular momentum → (3) ML²T⁻¹
- B. Torque → (4) ML²T⁻²
- C. Surface Tension → (2) MT⁻²
- D. Coefficient of viscosity → (1) ML⁻¹T⁻¹
Correct Code:
The correct matching code is 3 4 2 1.
- Definition: Angular momentum (L) is given by the formula L=M⋅V⋅R, where M is mass, V is velocity, and R is the radius (or distance).
- Dimensional Formula:
- Mass (M) has the dimension (M).
- Velocity (V) has the dimension (LT^{-1}).
- Radius (R) has the dimension (L).
Therefore, the dimensional formula for angular momentum is:
(L)=(M)⋅(LT−1)⋅(L)=(ML2T−1)
Conclusion: Angular momentum corresponds to (3) ML²T⁻¹.
- Definition: Torque (τ) is defined as the product of force and the distance from the pivot point, τ=F⋅R.
- Dimensional Formula:
- Force (F) has the dimension (MLT^{-2}).
- Distance (R) has the dimension (L).
Therefore, the dimensional formula for torque is:
(τ)=(F)⋅(L)=(MLT−2)⋅(L)=(ML2T−2)
Conclusion: Torque corresponds to (4) ML²T⁻².
- Definition: Surface tension (γ) is defined as force per unit length.
- Dimensional Formula:
- Force (F) has the dimension (MLT^{-2}).
- Length (L) has the dimension (L).
Therefore, the dimensional formula for surface tension is:
(γ)=(F)(L)=(MLT−2)(L)=(MT−2)
Conclusion: Surface tension corresponds to (2) MT⁻².
- Definition: The coefficient of viscosity (η) is defined as the ratio of shear stress to shear rate.
- Dimensional Formula:
- Shear stress has the dimension (MLT^{-2}) (force per unit area).
- Shear rate has the dimension (LT^{-1}).
Therefore, the dimensional formula for the coefficient of viscosity is:
(η)=(F/A)(V/L)=(MLT−2)(L2)⋅(LT−1)=(MLT−2)(L2)⋅(L)=(ML−1T−1)
Conclusion: Coefficient of viscosity corresponds to (1) ML⁻¹T⁻¹.
- A. Angular momentum → (3) ML²T⁻¹
- B. Torque → (4) ML²T⁻²
- C. Surface Tension → (2) MT⁻²
- D. Coefficient of viscosity → (1) ML⁻¹T⁻¹
The correct matching code is 3 4 2 1.
Topper's Solved these Questions
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:NDA EXAM QUESTIONS
Explore 55 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
Explore 24 Videos
- DIMENSIONSBook:ICSEChapter:DIMENSIONSExercise:SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
Explore 9 Videos
Similar Questions
Knowledge Check
Match List I with List II and select the correct answer by using the codes given below the lists:
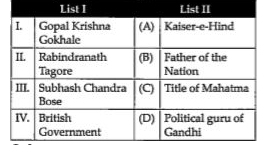 AI-D, II - A, III -B, IV-CBI-A, II – D, III -C, IV-BCI-A, II – D, III – B, IV-CDI-D, II -C, III – B, IV-A
AI-D, II - A, III -B, IV-CBI-A, II – D, III -C, IV-BCI-A, II – D, III – B, IV-CDI-D, II -C, III – B, IV-AMatch List I with List II and select the correct answer by using the codes given below the lists:

 AI-D, II - A, III - C, IV-BBI-B, II - D, III-A, IV-CCI-A, II – D, III – B, IV-CDI-D, II-A, III -B, IV-C
AI-D, II - A, III - C, IV-BBI-B, II - D, III-A, IV-CCI-A, II – D, III – B, IV-CDI-D, II-A, III -B, IV-CMatch List I with List II and select the correct answer by using the codes given below the lists:
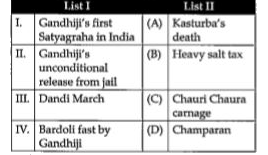 AI-D, II – A, III - C,IV-BBI-A, II-D, III -C, IV-BCI-A, II -D, III - B, IV-CDI-D, II-A, III -B, IV-C
AI-D, II – A, III - C,IV-BBI-A, II-D, III -C, IV-BCI-A, II -D, III - B, IV-CDI-D, II-A, III -B, IV-C
Match List I with List II and select the correct answer using codes given below the lists
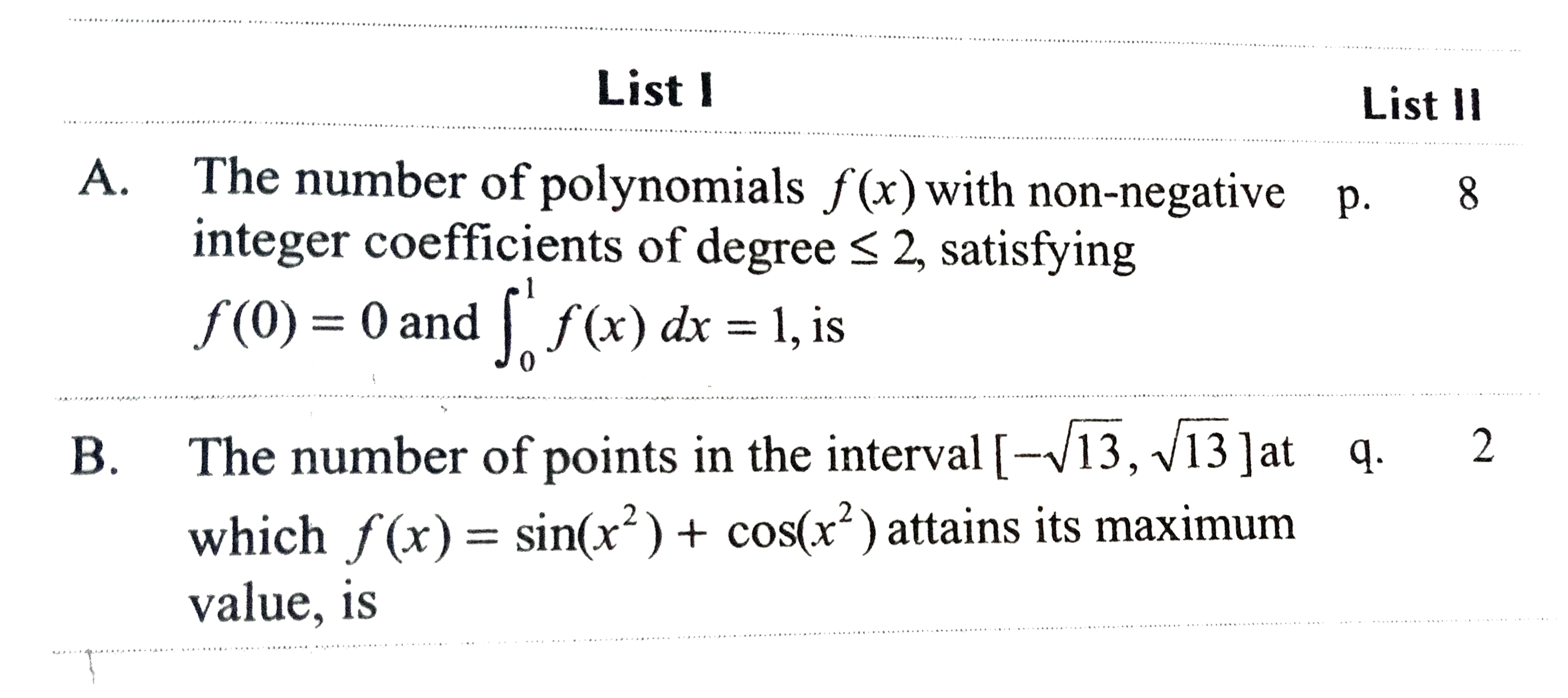
View SolutionMatch List I with List II and select the correct answer by using the codes given below the lists:
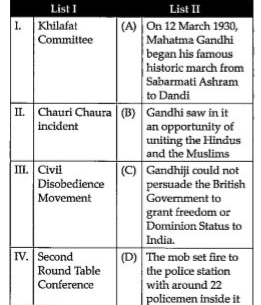
View SolutionMatch List I with List II and select the correct answer by using the codes given below the lists:
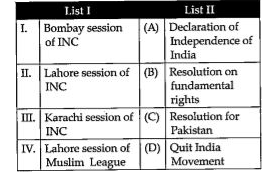
View SolutionMatch List I with List II and select the correct answer by using the codes given below the lists:
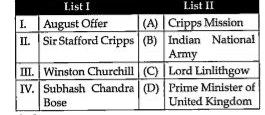
View SolutionMatch List I with List II and select the correct answer by using the codes given below the lists :

View Solution