The mass of a hoop of radius 0.30 m is 2kg. It rolls along a horizontal floor so that its centre of mass has a speed of 2 m/s. What is the work done to stop it ?
To solve the problem of finding the work done to stop a rolling hoop, we will follow these steps:
Step 1: Identify the parameters
- Mass of the hoop (m) = 2 kg
- Radius of the hoop (R) = 0.30 m
- Speed of the center of mass (V_cm) = 2 m/s
Step 2: Calculate the moment of inertia (I) of the hoop
For a hoop, the moment of inertia about its center of mass is given by the formula:
I=mR2
Substituting the values:
I=2kg×(0.30m)2
I=2×0.09
I=0.18kg m2
Step 3: Calculate the angular velocity (ω)
For pure rolling motion, the relationship between the linear velocity (V_cm) and angular velocity (ω) is given by:
Vcm=R⋅ω
Thus, we can rearrange this to find ω:
ω=VcmR=2m/s0.30m
ω=20.30
ω≈6.67rad/s
Step 4: Calculate the initial kinetic energy (KE_initial)
The total kinetic energy of the rolling hoop is the sum of its translational and rotational kinetic energies:
KEinitial=12mV2cm+12Iω2
Substituting the values:
KEinitial=12×2kg×(2m/s)2+12×0.18kg m2×(6.67rad/s)2
Calculating the translational kinetic energy:
KEtranslational=12×2×4=4J
Calculating the rotational kinetic energy:
KErotational=12×0.18×(6.67)2
KErotational=12×0.18×44.49≈4.00J
Thus, the total initial kinetic energy is:
KEinitial=4J+4J=8J
Step 5: Calculate the work done (W)
The work done to stop the hoop is equal to the initial kinetic energy since the final kinetic energy is zero:
W=KEinitial−KEfinal=8J−0=8J
Final Answer
The work done to stop the rolling hoop is 8 Joules.
---
- Mass of the hoop (m) = 2 kg
- Radius of the hoop (R) = 0.30 m
- Speed of the center of mass (V_cm) = 2 m/s
For a hoop, the moment of inertia about its center of mass is given by the formula:
I=mR2
Substituting the values:
I=2kg×(0.30m)2
I=2×0.09
I=0.18kg m2
For pure rolling motion, the relationship between the linear velocity (V_cm) and angular velocity (ω) is given by:
Vcm=R⋅ω
Thus, we can rearrange this to find ω:
ω=VcmR=2m/s0.30m
ω=20.30
ω≈6.67rad/s
The total kinetic energy of the rolling hoop is the sum of its translational and rotational kinetic energies:
KEinitial=12mV2cm+12Iω2
Substituting the values:
KEinitial=12×2kg×(2m/s)2+12×0.18kg m2×(6.67rad/s)2
KEtranslational=12×2×4=4J
KErotational=12×0.18×(6.67)2
KErotational=12×0.18×44.49≈4.00J
KEinitial=4J+4J=8J
The work done to stop the hoop is equal to the initial kinetic energy since the final kinetic energy is zero:
W=KEinitial−KEfinal=8J−0=8J
The work done to stop the rolling hoop is 8 Joules.
Topper's Solved these Questions
Similar Questions
A hoop of radius 2m weight 100kg.It rolls along a horizontal floor so that its centre of mass has a speed of 20cms−1. How much work has to be done to stop it ?
View SolutionA disc of radius 2 m and mass 100kg rolls on a horizontal floor, its centre of mass has speed of 20cm/s. How much work is needed to stop it ?
View Solution
Knowledge Check
A hoop of radius 2m weight 100kg.It rolls along a horizontal floor so that its centre of mass has a speed of 20cms−1. How much work has to be done to stop it ?
A2 JB4 JC6 JD8 J
A cylinder rolls on a horizontal plane surface. If the speed of the centre is 25 m/s, what is the speed of the highest point?
View Solution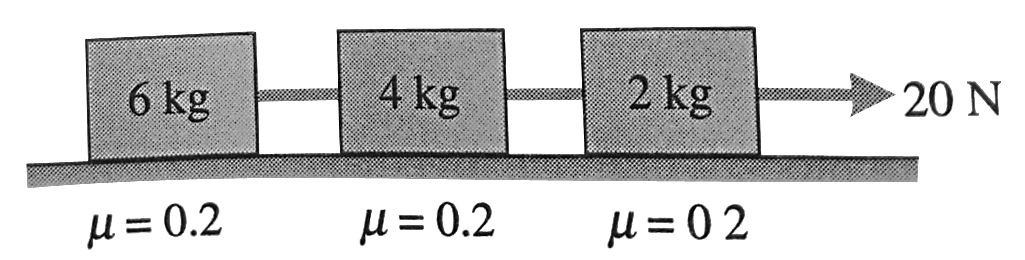
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. In the arrangement shoen tension in the string connecting 4 kg and 6 kg masses is
View SolutionA circular disc has a mass of 1kg and radius 40 cm. It is rotating about an axis passing through its centre and perpendicular to its plane with a speed of 10rev/s. The work done in joules in stopping it would be-
View SolutionA disc of radius R and mass m is projected on to a horizontal floor with a backward spin such that its centre of mass speed is v0 and angular velocity is ω0. What must be the minimum value of ω0 so that the disc eventually returns back?
View SolutionA uniform sphere of mass 500g rolls without slipping on a plane surface so that its centre moves at a speed of 0.02m/s.
The total kinetic energy of rolling sphere would be (in J)
View SolutionA person brings a mass of 1kg from infinity to a point A. Initially the mass was at rest but it moves with a speed of 2m/s as it reaches A. The work done by the person on a mass is −3J. The potential of A is:
View SolutionA person brings a mass of 1kg from infinity to a point A. Initially the mass was at rest but it moves with a speed of 2m/s as it reaches A. The work done by the person on a mass is −3J. The potential of A is:
View Solution
