A cylinder rolls on a horizontal plane surface. If the speed of the centre is 25 m/s, what is the speed of the highest point?
To find the speed of the highest point of a rolling cylinder, we can follow these steps:
1. Identify the Given Information:
- The speed of the center of the cylinder (V_cm) is given as 25 m/s.
2. Understand the Rolling Motion:
- When a cylinder rolls without slipping, the point of contact with the ground has zero velocity relative to the ground. This means that the velocity of the point of contact (point A) is equal to the velocity of the ground (point B), which is zero.
3. Relate Linear and Angular Velocity:
- For a rolling cylinder, the relationship between the linear velocity (V) of the center of mass and the angular velocity (ω) is given by:
V=ωr
- Here, r is the radius of the cylinder.
4. Determine the Velocity of the Highest Point:
- The highest point of the cylinder (let's call it point P) has two components of velocity:
- The translational velocity due to the center of mass, which is V_cm (25 m/s).
- The rotational velocity due to the rotation about the center, which is also ωr.
- Since V=ωr, we can substitute this into our equation for the highest point:
VP=Vcm+ωr
- Substituting ωr with V:
VP=Vcm+Vcm=2Vcm
5. Calculate the Speed of the Highest Point:
- Now, substituting the value of Vcm:
VP=2×25m/s=50m/s
Final Answer:
The speed of the highest point of the cylinder is 50 m/s.
---
- The speed of the center of the cylinder (V_cm) is given as 25 m/s.
- When a cylinder rolls without slipping, the point of contact with the ground has zero velocity relative to the ground. This means that the velocity of the point of contact (point A) is equal to the velocity of the ground (point B), which is zero.
- For a rolling cylinder, the relationship between the linear velocity (V) of the center of mass and the angular velocity (ω) is given by:
V=ωr
- Here, r is the radius of the cylinder.
- The highest point of the cylinder (let's call it point P) has two components of velocity:
- The translational velocity due to the center of mass, which is V_cm (25 m/s).
- The rotational velocity due to the rotation about the center, which is also ωr.
- Since V=ωr, we can substitute this into our equation for the highest point:
VP=Vcm+ωr
- Substituting ωr with V:
VP=Vcm+Vcm=2Vcm
- Now, substituting the value of Vcm:
VP=2×25m/s=50m/s
The speed of the highest point of the cylinder is 50 m/s.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
14 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
A sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then
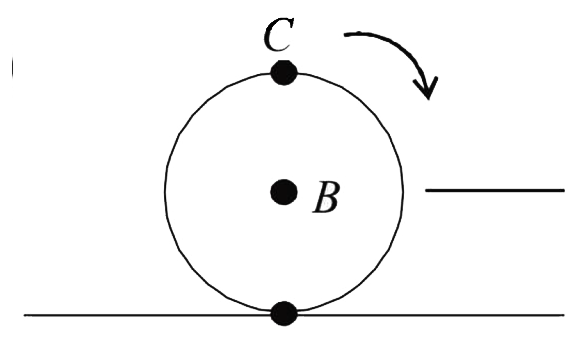
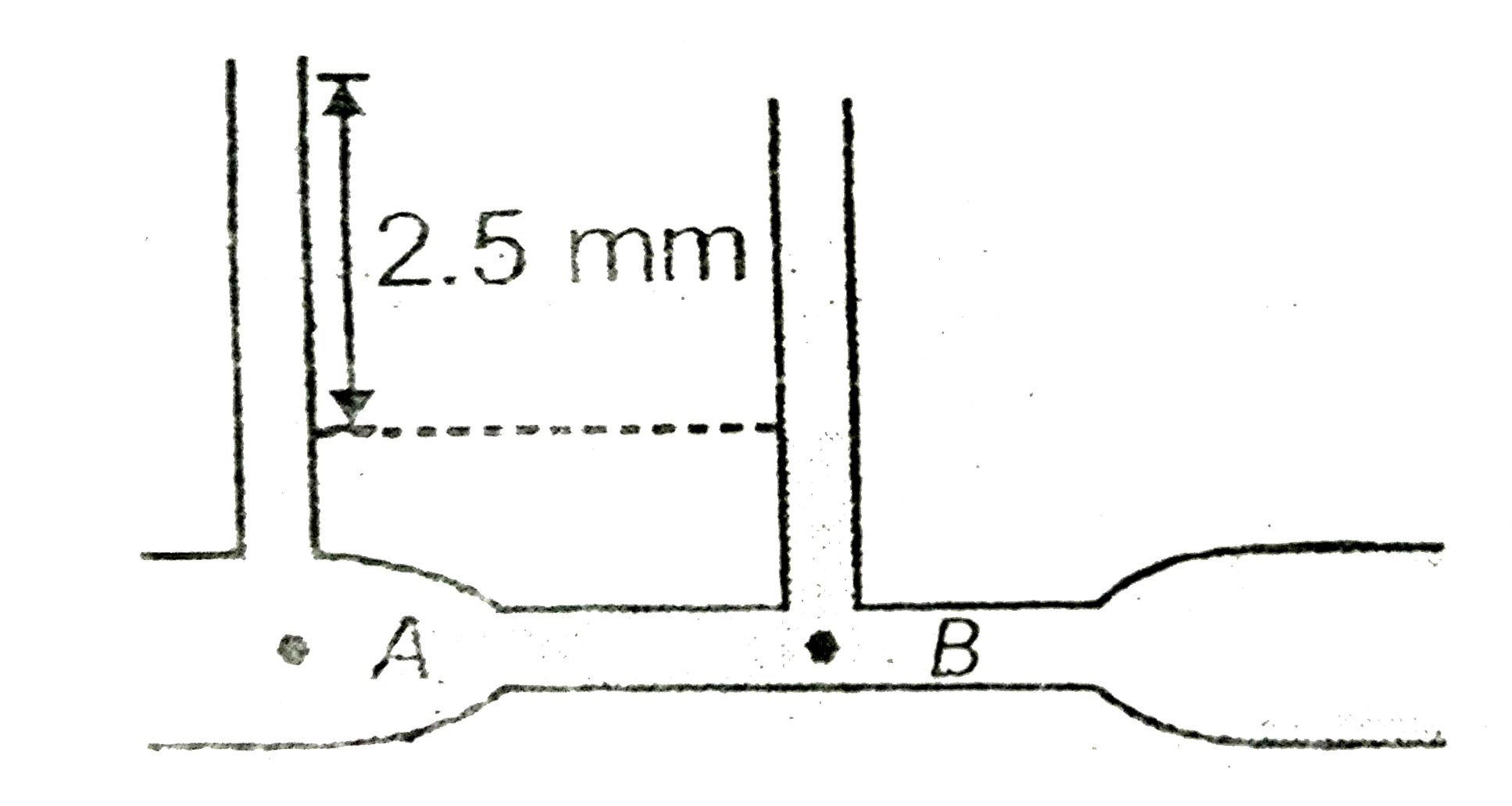
View SolutionIn the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?
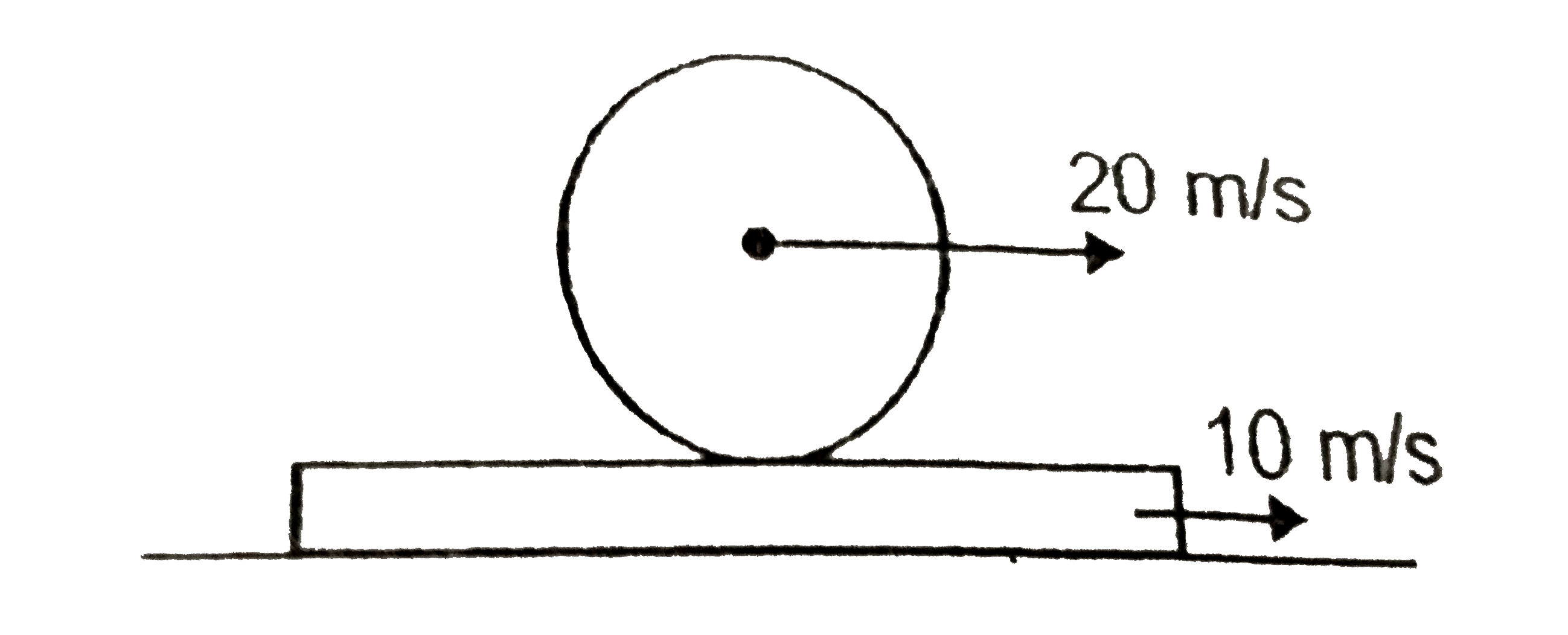
View SolutionA cylinder is rolling without slipping on a plank which is also moving with speed 10m/s on a horizontal surface as shown. The speed of centre of the cylinder is 20m/s. The mass of cylinder is 2kg. The kinetic energy of the cylinder when observed from ground is
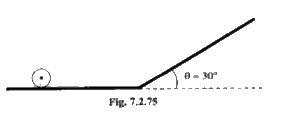
View SolutionA uniform solid sphere rolls on a horizontal surface with a linear speed of 10 m/s. It then rolls up a.plane inclined at 30° to horizontal. What is the height upto wlrich the sphere rises ? (See Fig.) Assume that the surface is frictionless. Also calculate the distance travelled by the Fig. sphere on the inclined plane ?
View SolutionThe mass of a hoop of radius 0.30 m is 2kg. It rolls along a horizontal floor so that its centre of mass has a speed of 2 m/s. What is the work done to stop it ?
View SolutionA disc is in the condition of pure rolling on the horizontal surface. The velocity of center of mass isV0 If radius of disc is R then the speed of point P is (OP=R3)
View SolutionA wheel ios rolling without sliding on a horizontal surface. The centre of the wheelk moves with a constant speed v0. Consider a point P on the rim which is at the top at time t=0. The square of speed of point P is plooted against time t. The correct plot is (R is radius of the wheel)
View SolutionA conducting rim of radius R rolls without slipping on a horizontal surface . The speed of the ring 's centre of mass is v0 . A uniform magnetic field B perpendicular to the ring 's plane is swithched on. The emf induced across point of contact and the topmost point of the rim is 2Bv0R.

View SolutionAir streams horizontally past an air plane. The speed over the top surface is 60 m/s, and that under the bottom surface is 45 m/s. The density of air is 1.293 kg/m3, then the difference in pressure
View SolutionA uniform disc of radius R is in pure rolling on a fixed horizontal surface with constant speed v0 as shown in the figure. For what value of θ, speed of point P will be v02√(5+2√3) ? (OP= R/2 and O is the centre of disc)

View Solution
