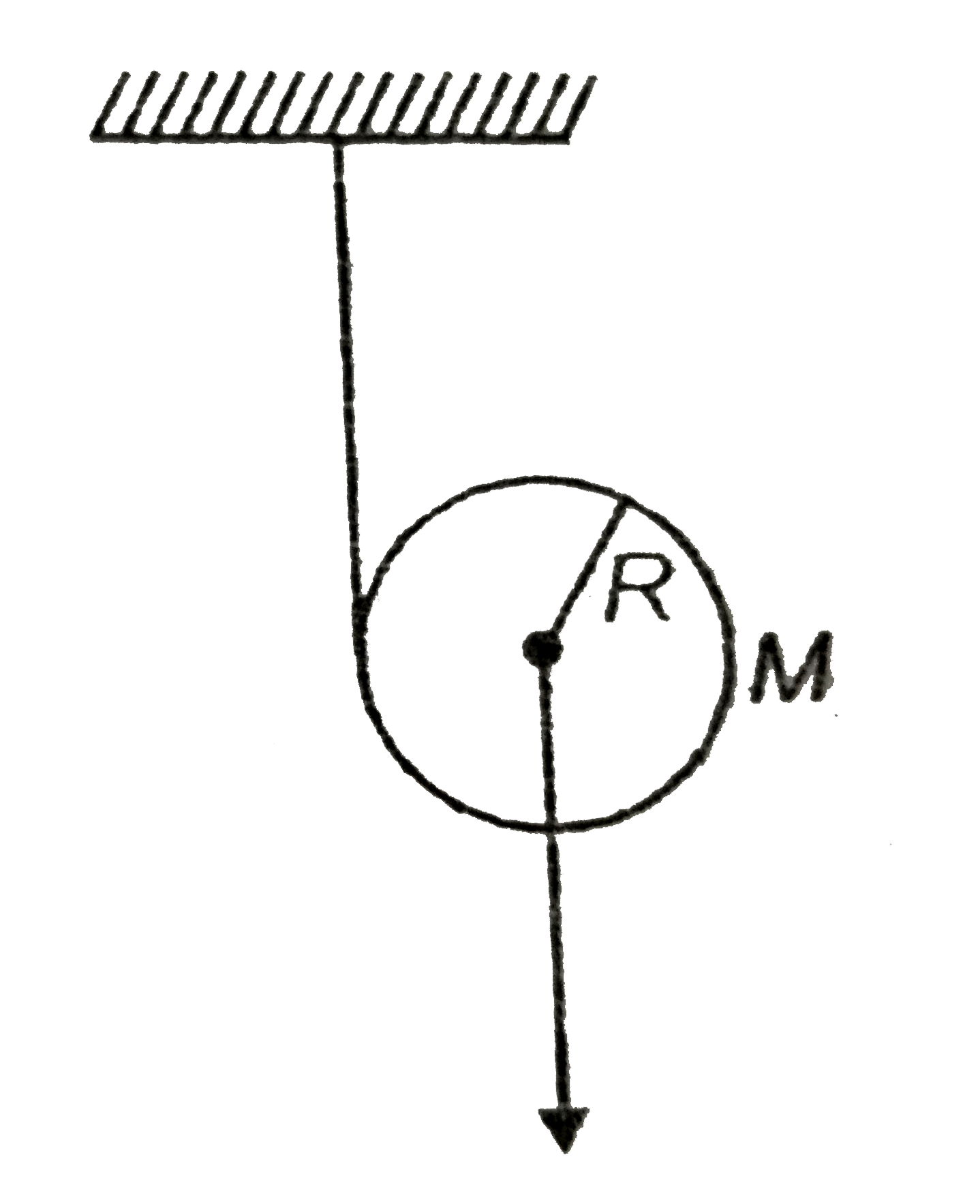
A string is wrapped over the edge a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
The correct Answer is:B, C
To find the downward acceleration of the disc, we can follow these steps:
Step 1: Identify the Forces Acting on the Disc
The forces acting on the disc are:
- The gravitational force (weight) acting downwards, which is mg.
- The tension force T in the string acting upwards.
Step 2: Apply Newton's Second Law
According to Newton's second law, the net force acting on the disc is equal to the mass of the disc multiplied by its acceleration:
ΣF=ma
The net force can be expressed as:
mg−T=ma(Equation 1)
Step 3: Relate Linear Acceleration to Angular Acceleration
The disc is rotating as it unwinds the string. The linear acceleration a of the disc is related to the angular acceleration α by the equation:
α=ar
where r is the radius of the disc.
Step 4: Calculate the Torque Acting on the Disc
The torque τ due to the tension T can be calculated as:
τ=T⋅r
According to the rotational form of Newton's second law, the torque is also equal to the moment of inertia I times the angular acceleration α:
τ=I⋅α
For a uniform disc, the moment of inertia I about its center is:
I=12mr2
Thus, we can write:
T⋅r=12mr2⋅α
Step 5: Substitute Angular Acceleration
Substituting α=ar into the torque equation gives:
T⋅r=12mr2⋅ar
Simplifying this, we get:
T⋅r=12mra
Dividing both sides by r:
T=12ma(Equation 2)
Step 6: Substitute Tension into the Force Equation
Now, substitute T from Equation 2 into Equation 1:
mg−12ma=ma
Rearranging gives:
mg=ma+12ma
mg=32ma
Step 7: Solve for Acceleration
Now, we can solve for a:
a=23g
Final Answer
The downward acceleration of the disc is:
a=23g
---
The forces acting on the disc are:
- The gravitational force (weight) acting downwards, which is mg.
- The tension force T in the string acting upwards.
According to Newton's second law, the net force acting on the disc is equal to the mass of the disc multiplied by its acceleration:
ΣF=ma
The net force can be expressed as:
mg−T=ma(Equation 1)
The disc is rotating as it unwinds the string. The linear acceleration a of the disc is related to the angular acceleration α by the equation:
α=ar
where r is the radius of the disc.
The torque τ due to the tension T can be calculated as:
τ=T⋅r
According to the rotational form of Newton's second law, the torque is also equal to the moment of inertia I times the angular acceleration α:
τ=I⋅α
For a uniform disc, the moment of inertia I about its center is:
I=12mr2
Thus, we can write:
T⋅r=12mr2⋅α
Substituting α=ar into the torque equation gives:
T⋅r=12mr2⋅ar
Simplifying this, we get:
T⋅r=12mra
Dividing both sides by r:
T=12ma(Equation 2)
Now, substitute T from Equation 2 into Equation 1:
mg−12ma=ma
Rearranging gives:
mg=ma+12ma
mg=32ma
Now, we can solve for a:
a=23g
The downward acceleration of the disc is:
a=23g
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
14 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
A disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
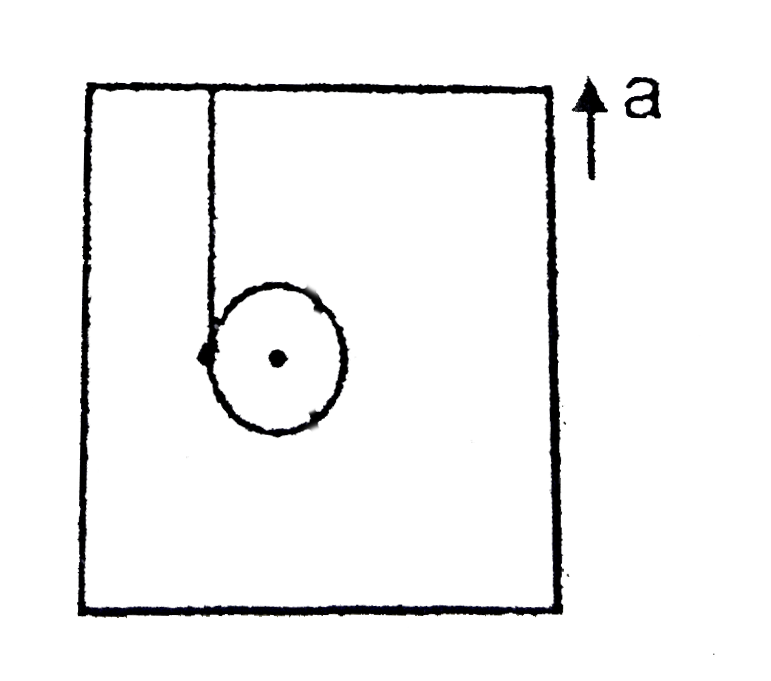
View SolutionIn the figure shown a thin light inextensible string is wrapped around a uniform disc. One end of the strin is fixed to the ceiling of the lift and the other end is fied to the circumference of the disc. Acceleration 'a' of the lift is such that the centre of the disc not move with respect to ground. Find the value of ag. String does not slip on pulley.
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionA wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionA string is wrapped on a uniform disc and the other end of the string connected to a wall. The system is placed on a smooth plane, inclined at an angle θ, with the string parallel to the plane, as shown in the figure. The acceleration of the disc is

View SolutionA uniform disc of mas M and radius R is smoothly pivoted at O. A light iextensible string wrapped over the disc hangs a particle of mass m. If the system is released from rest, assuming that the string does not slide on the disc, find the angular speed of the disc as the function of time using impulse momentum equation.

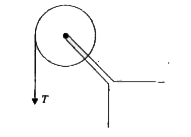
View SolutionFig. shows a uniform disc of mass 1 kg and radius 0.2 m mounted on an axle supported in fixed frictionless bearings. A light string is wrapped around the rim of the wheel. A constant downwards pull of 2 kg wt. is exerted on the string. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ?
View SolutionA uniform disc of radius R and mass M is free to rotate about a fixed horizontal axis perpendicular to its plane and passing through its centre. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The block is released from rest. If string does not slip on the rim then find the acceleration of the block. Neglect the mass of the string.
View Solution
