A uniform disc of mas M and radius R is smoothly pivoted at O. A light iextensible string wrapped over the disc hangs a particle of mass m. If the system is released from rest, assuming that the string does not slide on the disc, find the angular speed of the disc as the function of time using impulse momentum equation.

The net torque about O is
→τ=mgRˆk ………i
The angular momentum of the disc particle system about O is L=I0ω+mvR, where v=Rω
L=MR22ω+mR2ω=(MR22+mR2)ω
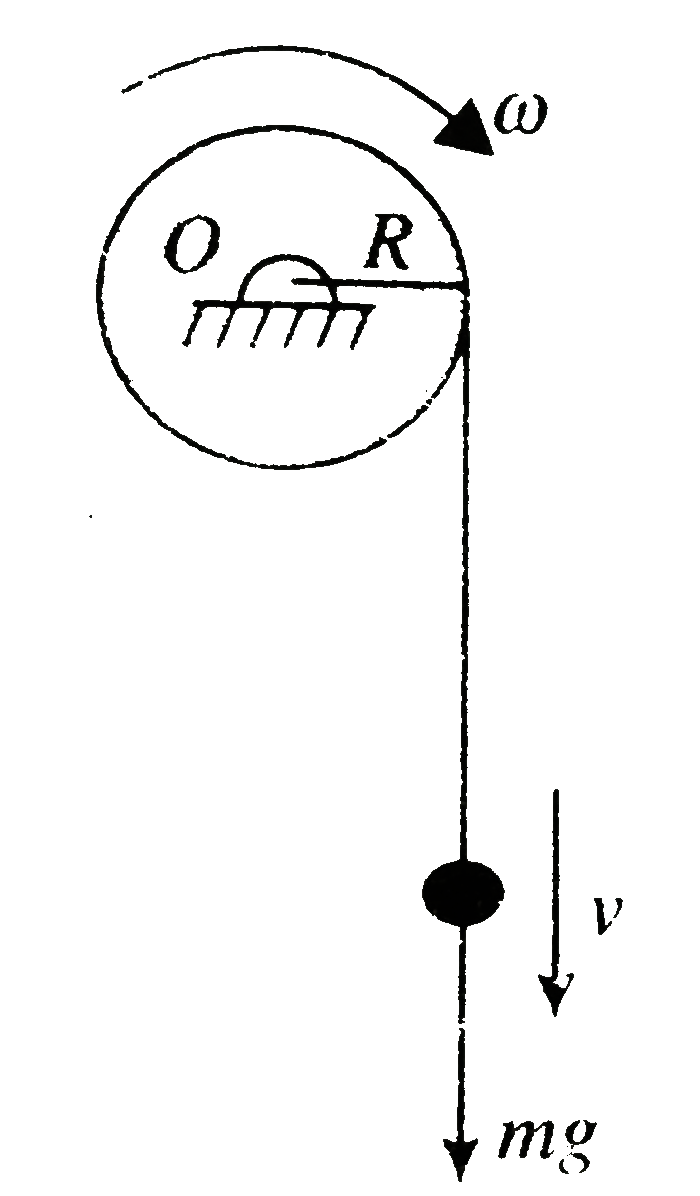
→L=(M+2m2)R2ωˆk.........ii
Impulse momentum equation is
△→OL=∫→τdt
Using eqn i , ii and ii we have
(M+2m2)R2ω=mgR∫10dt
ω=2mgt(M+2m)R
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions

A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionA uniform disc of mass M and radius R is liffted using a string as shown in the figure. Then choose incorrect option(s),

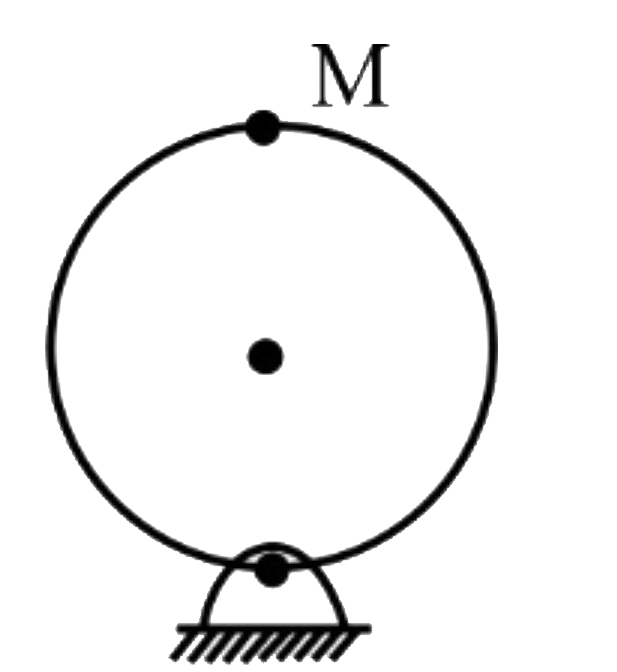
View SolutionA uniform disc of mass M and radius R is supported vertically by a pivot at its periphery as shown. A particle of mass M is fixed to the rim and raised to the highest point above the center. The system is released from rest and it can rotate about pivot freely. The angular speed of the system when the attached object is directly beneath the pivot, is
View SolutionA uniform disc of mass M and radius R is mounted on an axle supported in frictionless bearings. A light cord is wrapped around the rim of the disc and a steady downward pull T is exerted on the cord. The angular acceleration of the disc is
View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-

View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

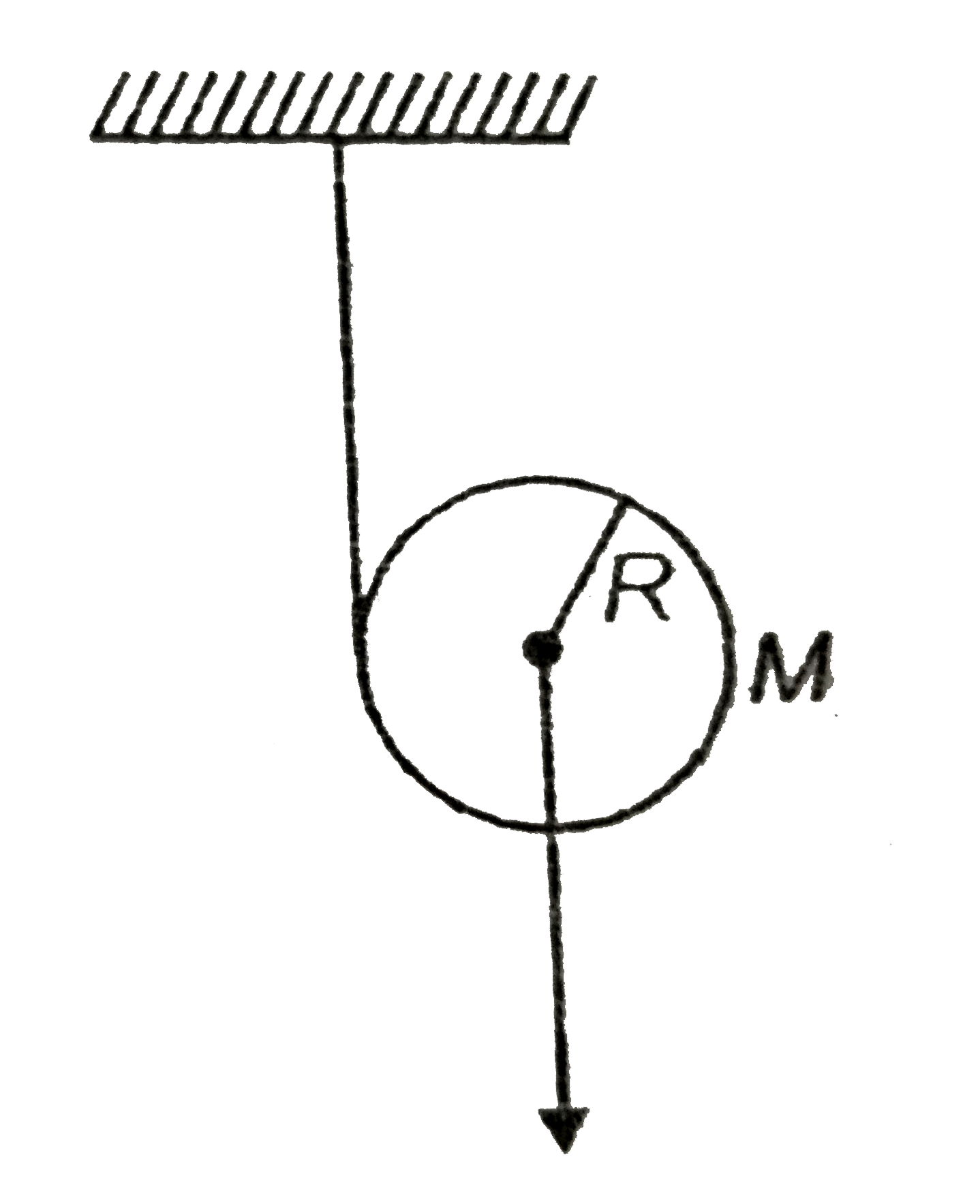
View SolutionA disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
View SolutionA uniform disc of radius R and mass M is free to rotate about a fixed horizontal axis perpendicular to its plane and passing through its centre. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The block is released from rest. If string does not slip on the rim then find the acceleration of the block. Neglect the mass of the string.
View Solution
