A circular discof mass 4 kg and radius 1 m rolls on a smooth table with a uniform velocity of 0.5ms−1. Calculate its (a) rotating K.E. (b) translational K.E.
To solve the problem, we need to calculate both the rotating kinetic energy and the translational kinetic energy of the circular disk.
Given Data:
- Mass of the disk, m=4kg
- Radius of the disk, r=1m
- Velocity of the disk, v=0.5m/s
(a) Rotating Kinetic Energy
1. Calculate the Moment of Inertia (I):
The moment of inertia I for a solid disk is given by the formula:
I=12mr2
Substituting the values:
I=12×4kg×(1m)2=12×4×1=2kg m2
2. Relate Angular Velocity (ω) to Linear Velocity (v):
For pure rolling motion, the relationship between linear velocity v and angular velocity ω is:
ω=vr
Substituting the values:
ω=0.5m/s1m=0.5rad/s
3. Calculate the Rotating Kinetic Energy (K.E.):
The formula for rotating kinetic energy is:
K.E.rot=12Iω2
Substituting the values:
K.E.rot=12×2kg m2×(0.5rad/s)2
K.E.rot=12×2×0.25=0.25J
(b) Translational Kinetic Energy
1. Calculate the Translational Kinetic Energy (K.E.):
The formula for translational kinetic energy is:
K.E.trans=12mv2
Substituting the values:
K.E.trans=12×4kg×(0.5m/s)2
K.E.trans=12×4×0.25=0.5J
Final Answers:
- Rotating Kinetic Energy: 0.25J
- Translational Kinetic Energy: 0.5J
- Mass of the disk, m=4kg
- Radius of the disk, r=1m
- Velocity of the disk, v=0.5m/s
The moment of inertia I for a solid disk is given by the formula:
I=12mr2
Substituting the values:
I=12×4kg×(1m)2=12×4×1=2kg m2
For pure rolling motion, the relationship between linear velocity v and angular velocity ω is:
ω=vr
Substituting the values:
ω=0.5m/s1m=0.5rad/s
The formula for rotating kinetic energy is:
K.E.rot=12Iω2
Substituting the values:
K.E.rot=12×2kg m2×(0.5rad/s)2
K.E.rot=12×2×0.25=0.25J
The formula for translational kinetic energy is:
K.E.trans=12mv2
Substituting the values:
K.E.trans=12×4kg×(0.5m/s)2
K.E.trans=12×4×0.25=0.5J
- Rotating Kinetic Energy: 0.25J
- Translational Kinetic Energy: 0.5J
Topper's Solved these Questions
Similar Questions
A disc of mass 5 kg and radius 50 cm rolls on the ground at the rate of 10ms−1. Calculate the K.E. of the disc.
View SolutionA uniform circular disc of mass m is set rolling on a smooth horizontal table with a uniform linear velocity v. Find the total K.E. of the disc.
View SolutionA uniform circular disc of mass 50kg and radius 0.4 m is rotating with an angular velocity of 10rads−1 about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (∈reds−1) of the system is
View SolutionA body of mass 5 kg is moving with velocity 2 ms−1. Calculate its linear momentum.
View SolutionA body of mass 5 kg is moving with velocity 2ms−1. Calculate its linear momentum.
View Solution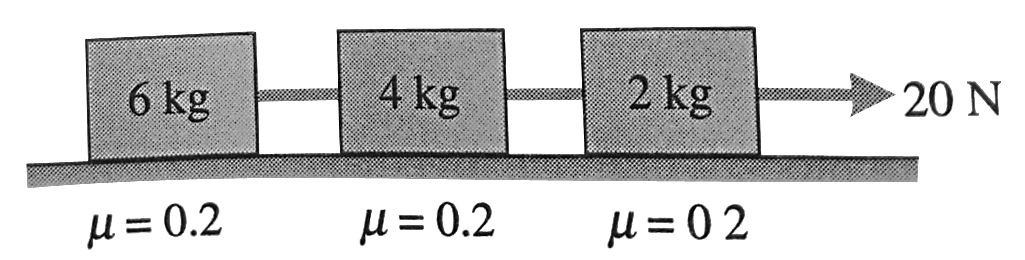
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. In the arrangement shoen tension in the string connecting 4 kg and 6 kg masses is
View SolutionIf a solid sphere of mass 1 kg and radius 0.1 m rolls without slipping at a uniform velocity of 1 m/s along a straight line on a horizontal floor, the kinetic energy is
View SolutionA disc of mass 4.8 kg and radius 1 m is rolling on a horizontal surface without sliding with angular velocity of 600 rotations/min. What is the total kinetic energy of the disc ?
View SolutionA ring of radius 0.5 m and mass 10 kg is rotating about its diameter with angular velocity of 20rads−1. Its kinetic energy is
View SolutionA disc of mass 1 kg and radius 0.1 m is rotating with angular velocity 20 rad s−1. What is angular velocity, if a mass of 0.25 kg is put on periphery of the disc?
View Solution

