A uniform circular disc of mass m is set rolling on a smooth horizontal table with a uniform linear velocity v. Find the total K.E. of the disc.
To find the total kinetic energy (K.E.) of a uniform circular disc of mass m that is rolling on a smooth horizontal table with a uniform linear velocity v, we need to consider both the translational kinetic energy and the rotational kinetic energy of the disc.
1. Identify the Types of Kinetic Energy:
- The total kinetic energy (K.E.) of the disc consists of two components:
- Translational K.E. due to its linear motion.
- Rotational K.E. due to its rotation about its own axis.
2. Calculate the Translational Kinetic Energy:
- The formula for translational kinetic energy is given by:
K.Etrans=12mv2
- Here, m is the mass of the disc and v is the linear velocity.
3. Calculate the Rotational Kinetic Energy:
- The moment of inertia I of a uniform circular disc about its own axis is:
I=12mr2
- The angular velocity ω can be related to the linear velocity v by the equation:
v=rω⇒ω=vr
- The rotational kinetic energy is given by:
K.Erot=12Iω2
- Substituting the expression for I and ω:
K.Erot=12(12mr2)(vr)2
- Simplifying this gives:
K.Erot=12⋅12mr2⋅v2r2=14mv2
4. Combine the Kinetic Energies:
- The total kinetic energy K.Etotal of the disc is the sum of the translational and rotational kinetic energies:
K.Etotal=K.Etrans+K.Erot
- Substituting the values we found:
K.Etotal=12mv2+14mv2
- Finding a common denominator:
K.Etotal=24mv2+14mv2=34mv2
5. Final Result:
- The total kinetic energy of the disc is:
K.Etotal=34mv2
- The total kinetic energy (K.E.) of the disc consists of two components:
- Translational K.E. due to its linear motion.
- Rotational K.E. due to its rotation about its own axis.
- The formula for translational kinetic energy is given by:
K.Etrans=12mv2
- Here, m is the mass of the disc and v is the linear velocity.
- The moment of inertia I of a uniform circular disc about its own axis is:
I=12mr2
- The angular velocity ω can be related to the linear velocity v by the equation:
v=rω⇒ω=vr
- The rotational kinetic energy is given by:
K.Erot=12Iω2
- Substituting the expression for I and ω:
K.Erot=12(12mr2)(vr)2
- Simplifying this gives:
K.Erot=12⋅12mr2⋅v2r2=14mv2
- The total kinetic energy K.Etotal of the disc is the sum of the translational and rotational kinetic energies:
K.Etotal=K.Etrans+K.Erot
- Substituting the values we found:
K.Etotal=12mv2+14mv2
- Finding a common denominator:
K.Etotal=24mv2+14mv2=34mv2
- The total kinetic energy of the disc is:
K.Etotal=34mv2
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
11 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (LONG ANSWER QUESTIONS)
8 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
A circular discof mass 4 kg and radius 1 m rolls on a smooth table with a uniform velocity of 0.5ms−1. Calculate its (a) rotating K.E. (b) translational K.E.
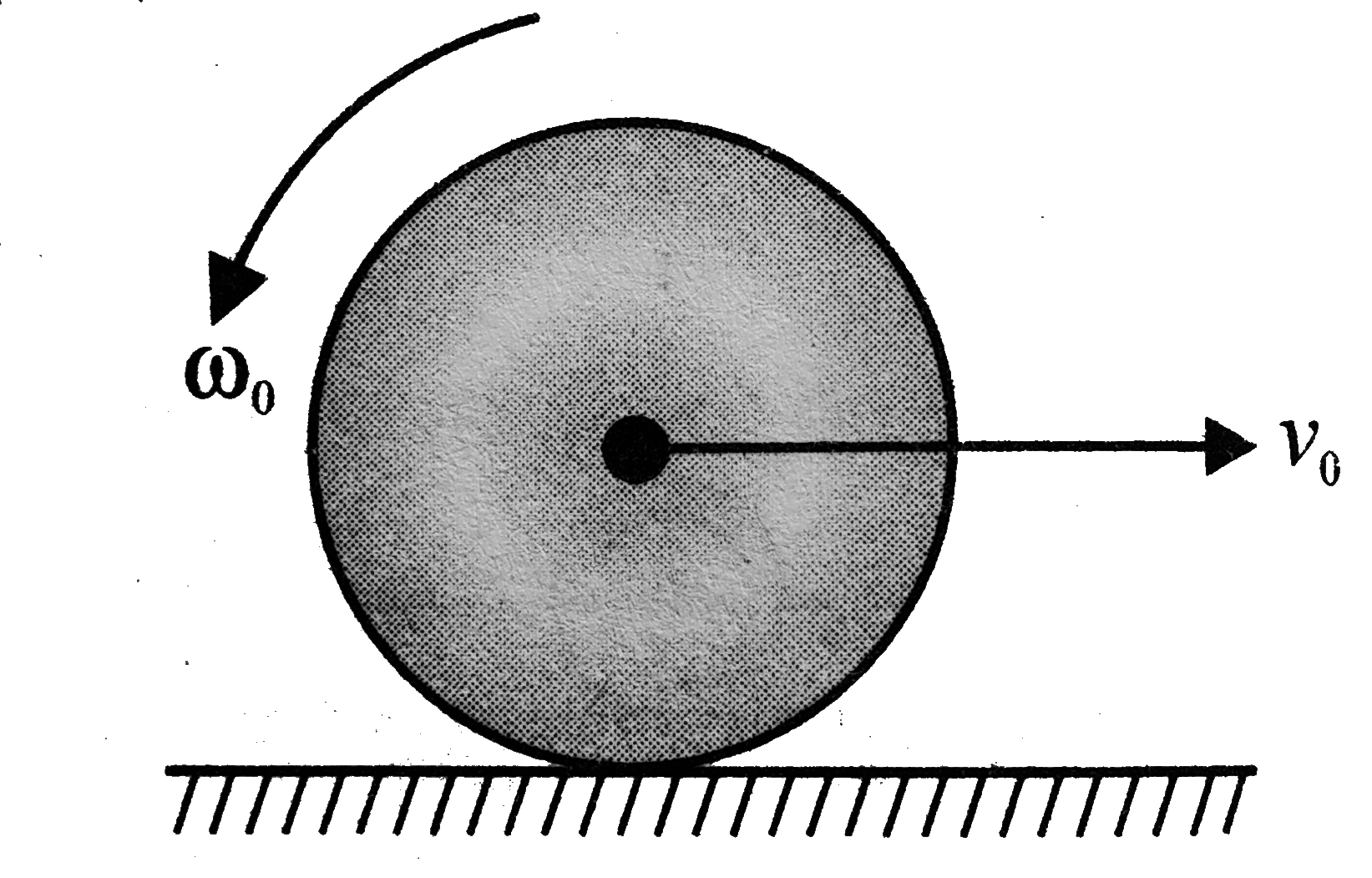
View SolutionA uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that
View SolutionA uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.
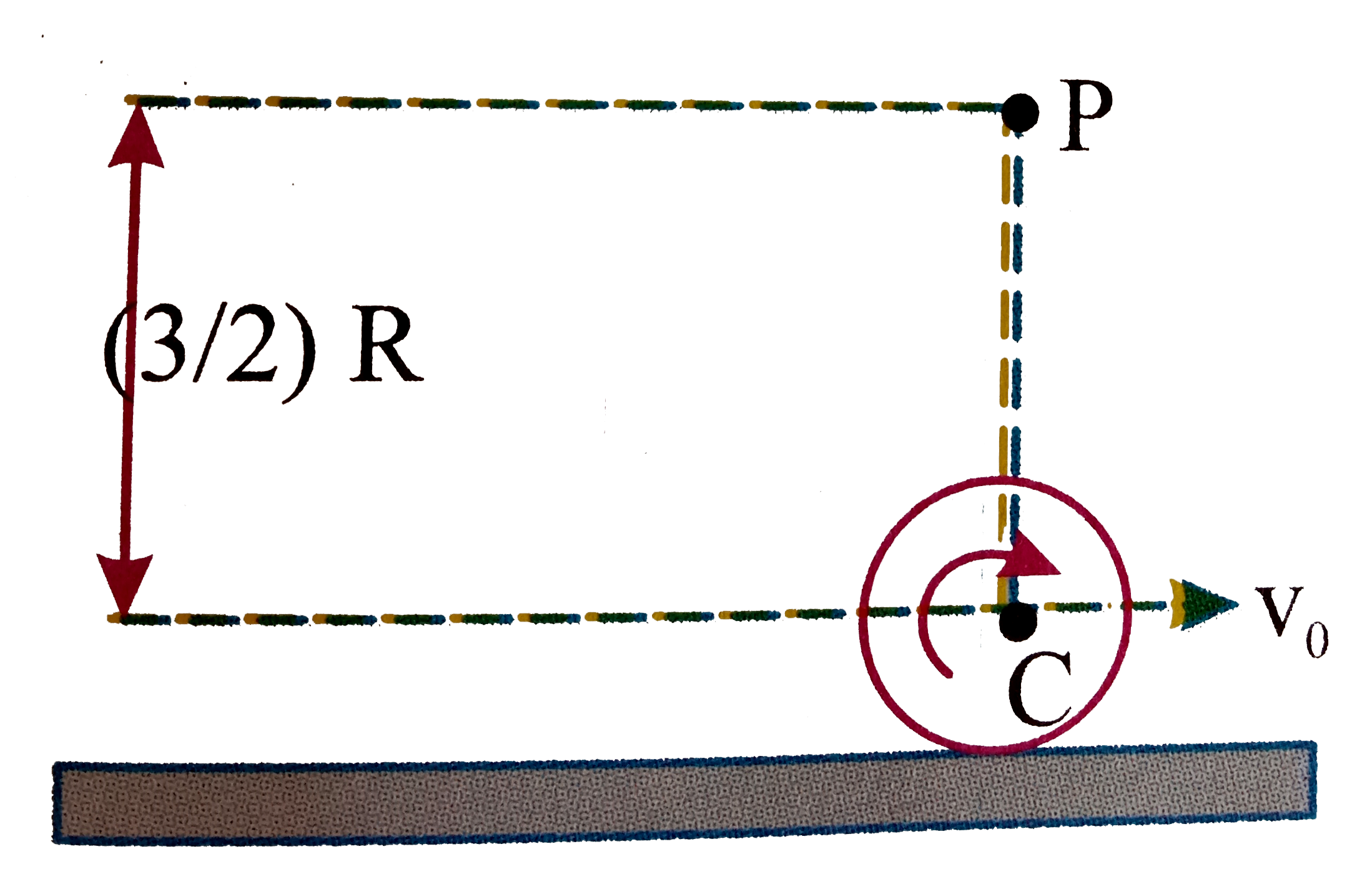
View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View Solution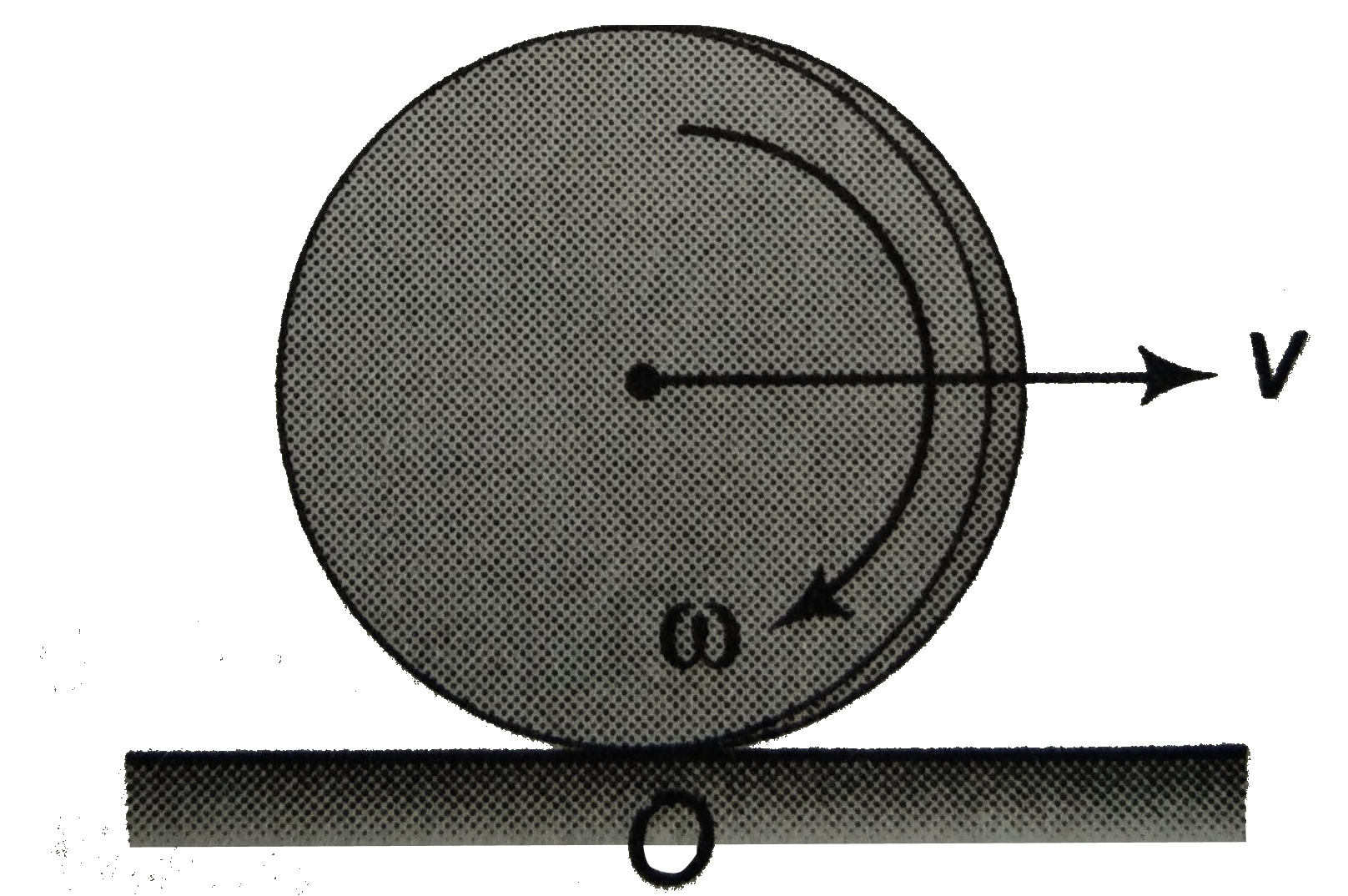
A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.
View Solution
A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.
View SolutionCharge Q is uniformly distributed on the rim of a thin insulating disc of mass m which is initially at rest and placed on a smooth horizontal surface. What will be the angular velocity of the disc if a magnetic field B, perpendicular to the plane of the disc is switched on ?

View Solutiona uniform circular disc of radiu8s r placed on a roughn horizontal plane has initial velocity v0 and an angul,ar velocity ω0 has shown The disc comes to rest after moving some distance in the direction of motion. Then

View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View Solution
