A disc of mass 5 kg and radius 50 cm rolls on the ground at the rate of 10ms−1. Calculate the K.E. of the disc.
To calculate the kinetic energy (K.E.) of a disc rolling on the ground, we need to consider both its translational and rotational kinetic energy. Here’s a step-by-step solution:
Step 1: Identify the given values
- Mass of the disc (m) = 5 kg
- Radius of the disc (r) = 50 cm = 0.5 m (convert to meters)
- Linear velocity of the center of mass (V_cm) = 10 m/s
Step 2: Calculate the moment of inertia (I) of the disc
The moment of inertia (I) of a disc about its center of mass is given by the formula:
I=12mr2
Substituting the values:
I=12×5kg×(0.5m)2
I=12×5×0.25
I=58kg m2
Step 3: Relate linear velocity to angular velocity
For a disc rolling without slipping, the relationship between linear velocity (V_cm) and angular velocity (ω) is:
Vcm=ωr
Thus, we can express angular velocity as:
ω=Vcmr=10m/s0.5m=20rad/s
Step 4: Calculate the rotational kinetic energy (K.E._rot)
The rotational kinetic energy is given by:
K.E.rot=12Iω2
Substituting the values:
K.E.rot=12×58kg m2×(20rad/s)2
K.E.rot=12×58×400
K.E.rot=5×2008=10008=125J
Step 5: Calculate the translational kinetic energy (K.E._trans)
The translational kinetic energy is given by:
K.E.trans=12mV2cm
Substituting the values:
K.E.trans=12×5kg×(10m/s)2
K.E.trans=12×5×100=5002=250J
Step 6: Calculate the total kinetic energy (K.E.)
The total kinetic energy is the sum of the translational and rotational kinetic energies:
K.E.=K.E.rot+K.E.trans
K.E.=125J+250J=375J
Final Answer
The kinetic energy of the disc is 375 Joules.
---
- Mass of the disc (m) = 5 kg
- Radius of the disc (r) = 50 cm = 0.5 m (convert to meters)
- Linear velocity of the center of mass (V_cm) = 10 m/s
The moment of inertia (I) of a disc about its center of mass is given by the formula:
I=12mr2
Substituting the values:
I=12×5kg×(0.5m)2
I=12×5×0.25
I=58kg m2
For a disc rolling without slipping, the relationship between linear velocity (V_cm) and angular velocity (ω) is:
Vcm=ωr
Thus, we can express angular velocity as:
ω=Vcmr=10m/s0.5m=20rad/s
The rotational kinetic energy is given by:
K.E.rot=12Iω2
Substituting the values:
K.E.rot=12×58kg m2×(20rad/s)2
K.E.rot=12×58×400
K.E.rot=5×2008=10008=125J
The translational kinetic energy is given by:
K.E.trans=12mV2cm
Substituting the values:
K.E.trans=12×5kg×(10m/s)2
K.E.trans=12×5×100=5002=250J
The total kinetic energy is the sum of the translational and rotational kinetic energies:
K.E.=K.E.rot+K.E.trans
K.E.=125J+250J=375J
The kinetic energy of the disc is 375 Joules.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A circular discof mass 4 kg and radius 1 m rolls on a smooth table with a uniform velocity of 0.5ms−1. Calculate its (a) rotating K.E. (b) translational K.E.
View SolutionA uniform circular disc of mass 50kg and radius 0.4 m is rotating with an angular velocity of 10rads−1 about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (∈reds−1) of the system is
View SolutionA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View Solution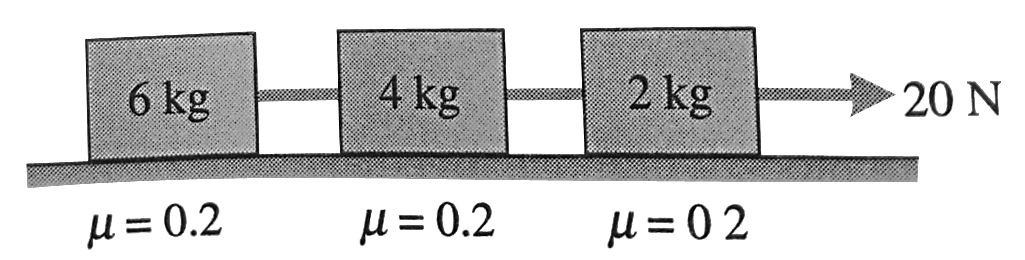
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. In the arrangement shoen tension in the string connecting 4 kg and 6 kg masses is
View SolutionA disc of mass 1 kg and radius 0.1 m is rotating with angular velocity 20 rad s−1. What is angular velocity, if a mass of 0.25 kg is put on periphery of the disc?
View SolutionA disc of mass 2 kg and radius 0.2 m is rotating with angular velocity 30rad s−1. What is angular velocity, if a mass of 0.25 kg is put on periphery of the disc ?
View SolutionA uniform disc of mass 20 kg and radius 0.5 m can turn about a smooth axis through its centre and perpendicular to the disc. A constant torque is applied to the disc for 3s from rest and the angular velocity at the ned of that time is 240πrev/min find the magnitude of the torque. if the torque is then removed and the disc is brought to rest in t seconds by a constant force of 10 N applied tangentially at a point on the rim of the disc, find t
View SolutionA uniform disc of mass 1kg and radius 20cm is rolling purely on a flat horizontal surface. Its centre C is moving with acceleration a=20ms−2 and velocity v=4m/s at a certain instant. At this instant. points A and B are located on the disc as shown in the diagram, with AC=BC=10cm.

What is the kinetic energy of the disc?
View SolutionCalculate the moment of inertia of a.unifprm disc of mass 0.4 kg and radius 0.1m about an axis passing through its edge and perpendicular to the plane of die disc ?
View SolutionA circular disc of 49 kg and radius 50 cm is rotating at a speed of 120 rotations per minute. Calculate its kinetic energy if is moment of inertia about the axis of rotation is 12mr2.
View Solution
