If two circular discs A and B are of same mass but of radii r and 2r respectively, then the moment of inertia of A is
the same as that of B
twice that of B
four times that of B
one-fourth that of B
The correct Answer is:D
To find the moment of inertia of two circular discs A and B with the same mass but different radii, we can follow these steps:
Step 1: Understand the formula for moment of inertia
The moment of inertia I for a circular disc about its central axis is given by the formula:
I=12mr2
where m is the mass of the disc and r is its radius.
Step 2: Calculate the moment of inertia for disc A
For disc A, the radius is r and the mass is m. Therefore, the moment of inertia IA is:
IA=12mr2
Step 3: Calculate the moment of inertia for disc B
For disc B, the radius is 2r and the mass is also m. Therefore, the moment of inertia IB is:
IB=12m(2r)2
Calculating this gives:
IB=12m(4r2)=2mr2
Step 4: Compare the moments of inertia
Now, we can compare IA and IB:
IA=12mr2
IB=2mr2
Step 5: Express IA in terms of IB
To find the relationship between IA and IB, we can express IB in terms of IA:
IB=4(12mr2)=4IA
Thus, we can write:
IA=14IB
Conclusion
The moment of inertia of disc A is one-fourth that of disc B.
Final Answer
The moment of inertia of A is one-fourth that of B.
---
The moment of inertia I for a circular disc about its central axis is given by the formula:
I=12mr2
where m is the mass of the disc and r is its radius.
For disc A, the radius is r and the mass is m. Therefore, the moment of inertia IA is:
IA=12mr2
For disc B, the radius is 2r and the mass is also m. Therefore, the moment of inertia IB is:
IB=12m(2r)2
Calculating this gives:
IB=12m(4r2)=2mr2
Now, we can compare IA and IB:
IA=12mr2
IB=2mr2
To find the relationship between IA and IB, we can express IB in terms of IA:
IB=4(12mr2)=4IA
Thus, we can write:
IA=14IB
The moment of inertia of disc A is one-fourth that of disc B.
The moment of inertia of A is one-fourth that of B.
Topper's Solved these Questions
Similar Questions
Two circular loops A and B of radii R and 2R respectively are made of the similar wire. Their moments of inertia about the axis passing through the centre of perpendicular to their plane are IA and IB respectively. The ratioIAIB is :
View SolutionTwo circular discs are of same thickness. The diameter of A is twice that of B. The moment of inertia of A as compared to that of B is
View SolutionTwo uniform circular loops A and B of radii r and nr are made of the same uniform wire. If moment of inertia of A about its axis is twice that of B, then find the value of n [diameter of wire is much smaller compared to radii of the loops].
View SolutionTwo discs A and B have same mass and same thickness. If d1 and d2 are the densities of the materials of the discs A and B respectively, then the ratio of the moment of inertia of the discs A and B about their geometrical axis is
View SolutionOne circular ring and one circular disc, both are having the same mass and radius. The ratio of their moments of inertia about the axes passing through their centres and perpendicular to their planes, will be
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
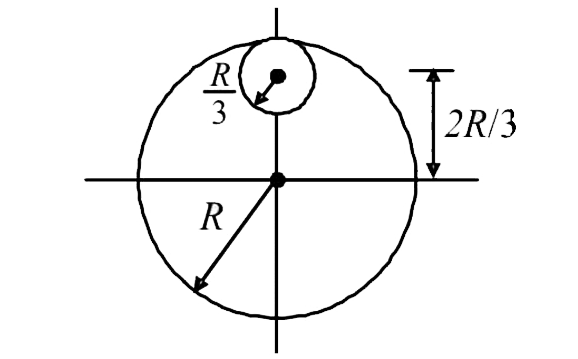
View SolutionThe radii of circular orbits of two satellite A and B of the earth are 4R and R, respectively. If the speed of satellite A is 3v, then the speed of satellite B will be
View SolutionA disc of mass m and radius R is attached to a rectangular plate of the same mass m, breadth R and length 2R as shown in figure. The moment of inertia of the system about the axis AB passing through the centre of the disc and along the plane is I=1α(313mR2).
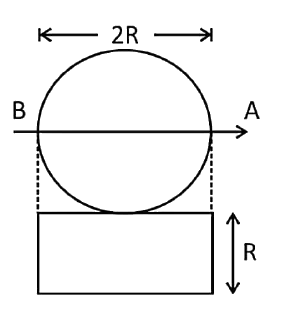
View SolutionTwo satellites A and B go around a planet in circular orbits of radii 4 R and R respectively. If the speed of the satellite A is 3 V, then the speed of the satellite B will be
View SolutionTwo loops P and Q are made from a uniform wire. The radii of P and Q are R1 and R2, respectively, and their moments of inertia about their axis of rotation are I1 and I2, respectively. If I1I2=4, then R2R1 is
View Solution
