Assertion : Moment of inertia about an axis passing throught centre of mass is always minimum
Reason : Theorem of parallel axis can be applied for 2-D as well as 3-D bodies.
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion
If Assertion is true but Reason is fasle
If Assertion is false but Reason is true
The correct Answer is:B
To solve the question, we need to analyze the assertion and reason provided.
Step 1: Understand the Assertion
The assertion states that the moment of inertia about an axis passing through the center of mass is always minimum. This is a fundamental principle in physics. The moment of inertia (I) is a measure of an object's resistance to changes in its rotation. When the axis of rotation is at the center of mass, the distribution of mass relative to that axis is such that the moment of inertia is minimized.
Hint: Recall the definition of moment of inertia and how it depends on the distribution of mass relative to the axis of rotation.
Step 2: Understand the Reason
The reason states that the theorem of parallel axes can be applied for both 2-D and 3-D bodies. The parallel axis theorem states that the moment of inertia about any axis parallel to an axis through the center of mass can be calculated using the formula:
I=Icm+Md2
where Icm is the moment of inertia about the center of mass, M is the mass of the body, and d is the distance between the two axes.
Hint: Think about how the parallel axis theorem is used to calculate moments of inertia for different axes and how it applies to both 2-D and 3-D objects.
Step 3: Analyze the Relationship Between Assertion and Reason
While both the assertion and reason are true, the reason does not explain why the moment of inertia is minimum at the center of mass. The minimum moment of inertia at the center of mass is due to the nature of mass distribution, not merely because the parallel axis theorem applies to both 2-D and 3-D bodies.
Hint: Consider how the parallel axis theorem relates to the distribution of mass and how that affects the moment of inertia.
Conclusion
Both the assertion and reason are true, but the reason is not the correct explanation for the assertion. Therefore, the correct answer to the question is that both statements are true, but the reason does not adequately explain the assertion.
Final Answer: Option B is correct: Both assertion and reason are true, but the reason is not the correct explanation of the assertion.
The assertion states that the moment of inertia about an axis passing through the center of mass is always minimum. This is a fundamental principle in physics. The moment of inertia (I) is a measure of an object's resistance to changes in its rotation. When the axis of rotation is at the center of mass, the distribution of mass relative to that axis is such that the moment of inertia is minimized.
The reason states that the theorem of parallel axes can be applied for both 2-D and 3-D bodies. The parallel axis theorem states that the moment of inertia about any axis parallel to an axis through the center of mass can be calculated using the formula:
I=Icm+Md2
where Icm is the moment of inertia about the center of mass, M is the mass of the body, and d is the distance between the two axes.
While both the assertion and reason are true, the reason does not explain why the moment of inertia is minimum at the center of mass. The minimum moment of inertia at the center of mass is due to the nature of mass distribution, not merely because the parallel axis theorem applies to both 2-D and 3-D bodies.
Both the assertion and reason are true, but the reason is not the correct explanation for the assertion. Therefore, the correct answer to the question is that both statements are true, but the reason does not adequately explain the assertion.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (A) Chapter Exercises
83 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Knowledge Check
For the same total mass, which of the following will have the largest moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the body a) A disc of radius a b) A ring of radius a c) A square lamina of side a d) Four identical rods forming square of side a
AA disc of radius aBA ring of radius aCA square lamina of side aDFour identical rods forming square of side a
find moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown
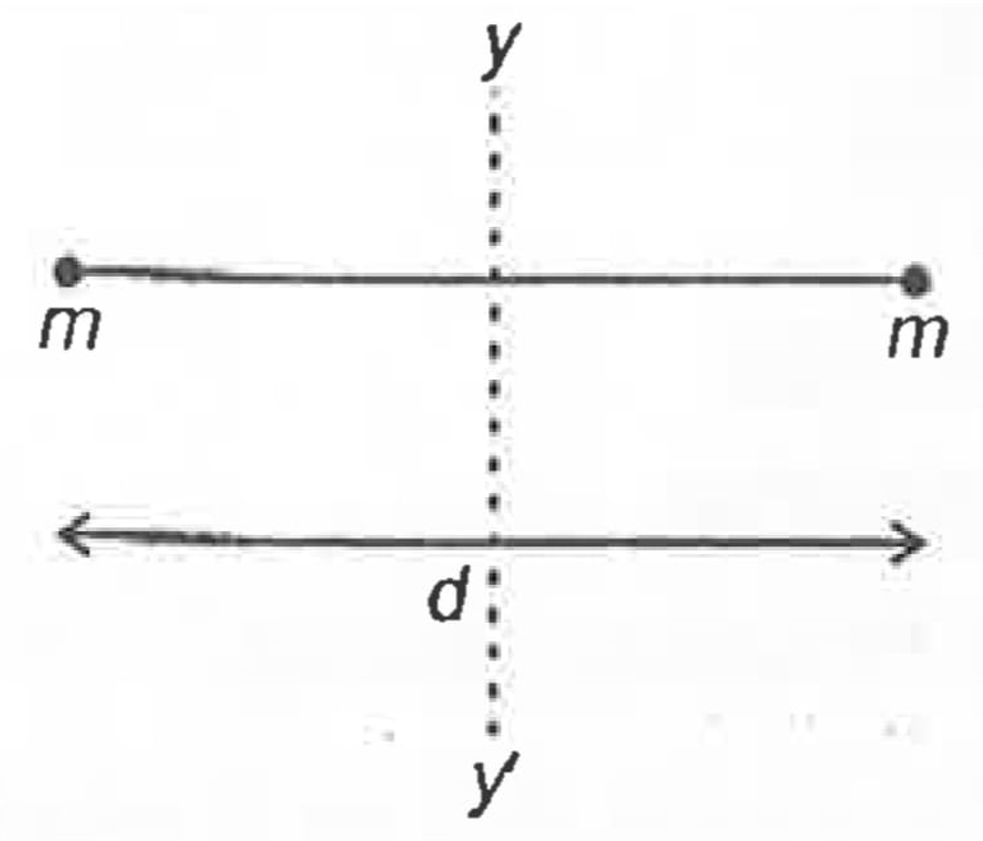
View SolutionFor the structure shown in figure, moment of inertia about an axis passing through yy' is
_PHY_213_Q01.png)
View SolutionA solid sphere of mass M, radius R and having moment of inertia about as axis passing through the centre of mass as I, is recast into a disc of thickness t, whose moment of inertia about an axis passing through its edge and perpendicular to its plance remains I. Then, radius of the disc will be.
View SolutionFor the structure shown in figure, moment of inertia about an Axis passing through yy' is
_PHY_E05_238_Q01.png)
View SolutionTwo point masses m and 3m are placed at distance r. The moment of inertia of the system about an axis passing through the centre of mass of system and perpendicular to the joining the point masses is
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View Solution
