Two coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
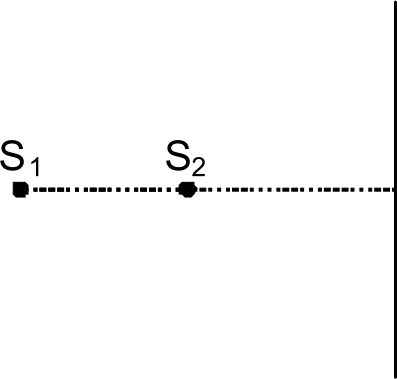
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 is
For S1S2=2.5λ, max path difference =2.5λ
min path difference =0
Between 2.5λ and 0 lie 2λ and λ⇒ two circular bright fringes
n1=2
For S1S2=5.7λ, max path difference =5.7λ
min path difference =0
Between 5.7λ and 0 lie 5λ,4λ,2λ,λ⇒ five circular bright fringes.
⇒n2=5
∴n2−n1=5−2=3
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two points nonochromatic and coherent sources of light of wavelength λ each are placed as shown in figure. The initial phase difference between the sources is zero O. (d>>d). Mark the correct statement(s).
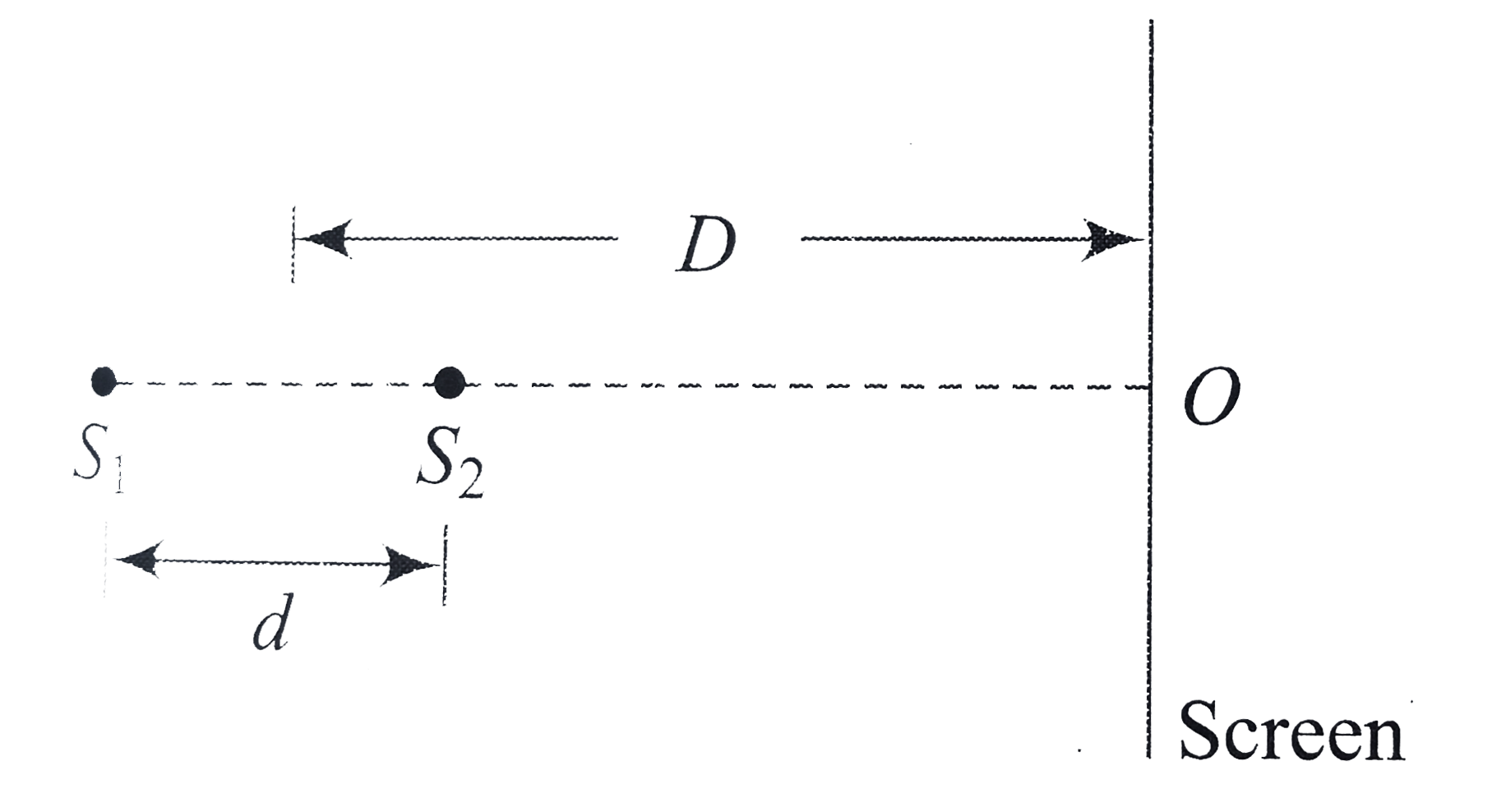 AIf d=7λ2,O will be minima.BIf d=λ, only one maxima can be observed on screen.CIf d=4.8λ then total 10 minimas would be there on screen.DIf d=5λ2, then intensity at O would be maximum.
AIf d=7λ2,O will be minima.BIf d=λ, only one maxima can be observed on screen.CIf d=4.8λ then total 10 minimas would be there on screen.DIf d=5λ2, then intensity at O would be maximum.
Two coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
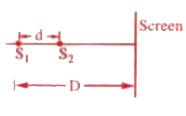
View SolutionAssertion: Two coherent sources S1andS2 are placed in front of a screen as shown in figure. At point P, 10th order maxima is obtained. Then , 11th order maxima will be obtained above P.
Reason: For 11th order maxima path difference should be more.
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between them is 2λ as shown in figure. The first bright fringe is formed at .P. due to interference on a screen placed at a distance .D. from S1 (D>>λ), then OP is

View SolutionS1 and S2 are two sources of sound emitting sine waves. The two sources are in phase. The sound emitted by the two sources interfers at point F. The waves of wavelength :

View SolutionTwo coherent sources S1 and S2 produce interference fringes. If a thin mica plate is introduced in the path of light from S1 then the central maximum
View SolutionTwo coherent light sources S1 and S2(λ=6000Å) are 1mm apart from each other. The screen is placed at a distance of 25cm from the sources. The width of the fringes on the screen should be
View SolutionIf S1andS2 are two point sources emitting light in phase , then what is the shape of interference fringes formed on the screen ?
View Solution

