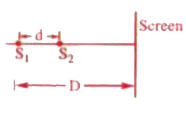
Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

ellipse
straight lines
hyperbolas
concentric circles
The correct Answer is:D
Step by step video & image solution for Two coherent point sources S_1 and S_2 are separated by a small distance d as shown. The fringes obtained on the screen will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced Only one option is correct22videos
WAVE OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced B. More than one option is correct4videos
WAVE OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - medical entrances42videos
WAVE OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - JIPMER22videos
SOLVED PAPERS 2018
Similar Questions
Two coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
 View Solution
View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance L. Each sources emits light of wavelength λ, where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Then
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionStatement I: Two coherent point sources of light having no-zero phase difference are separated by a small distance. Then, on the perpendicular bisector of line segment joining both the point sources, constructive interference cannot be obtained.
Statement II: For two waves from coherent point sources to interfere constructively at a point, the magnitude of their phase difference at that point must be 2mπ (where m is non-negative integer).View SolutionAssertion: Two coherent sources S1andS2 are placed in front of a screen as shown in figure. At point P, 10th order maxima is obtained. Then , 11th order maxima will be obtained above P.
Reason: For 11th order maxima path difference should be more.View SolutionConsider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between the sources is 2λ. The smallest distance from S2 on a line passing through S2 and perpendicular to s1s2 where a minimum of intensity occurs is
View SolutionTwo coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
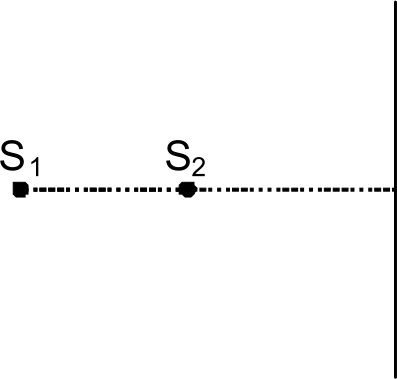
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 isView SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .View Solution
.View SolutionTwo coherent source of light can be obtained by
View Solution
