Question

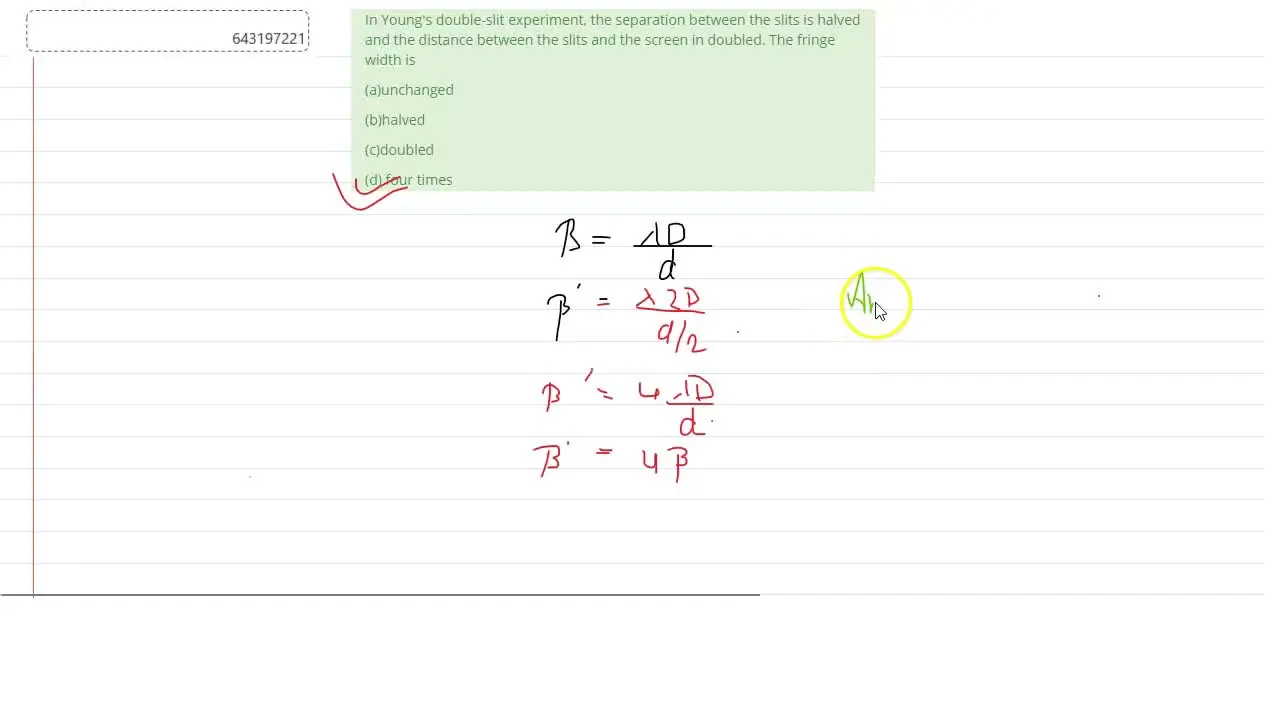
In Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is

Options

A. (a)unchanged
B. (b)halved
C. (c)doubled
D. (d) four times

Answer

D

Explanation

To solve the problem regarding the fringe width in Young's double-slit experiment, we start with the formula for fringe width (β):

Step 1: Write the formula for fringe width
The fringe width (β) is given by the formula:
\( \beta = \frac{\lambda D}{d} \)
where:
- \( \lambda \) = wavelength of light
- \( D \) = distance from the slits to the screen
- \( d \) = separation between the slits

Step 2: Analyze the changes in the experiment
According to the problem:
- The separation between the slits (d) is halved: \( d' = \frac{d}{2} \)
- The distance from the slits to the screen (D) is doubled: \( D' = 2D \)

Step 3: Substitute the new values into the fringe width formula
Now, we can find the new fringe width (β'):
\( \beta' = \frac{\lambda D'}{d'} \)
Substituting the new values:
\( \beta' = \frac{\lambda (2D)}{\frac{d}{2}} = \frac{\lambda \cdot 2D \cdot 2}{d} = \frac{4\lambda D}{d} \)

Step 4: Relate the new fringe width to the original fringe width
Now, we can express the new fringe width in terms of the original fringe width (β):
\( \beta' = 4 \beta \)
This means that the new fringe width is four times the original fringe width.

Conclusion
Thus, the fringe width after the changes is:
\( \beta' = 4 \beta \)

Final Answer
The fringe width is increased by a factor of 4.

---