Two monochromatic coherent point sources and are separated by a distance L. Each sources emits light of wavelength , where . The line when extended meets a screen perpendicular to it at point A. Then
the interference fringe on the screen are straight lines shape
the interference fringes on the screen are strainght lines perpendicular to the line
point A is an intensity maxima if
point A is always an intensity maxima for any separation L
The correct Answer is:c
To solve the problem, we need to analyze the interference pattern created by two coherent point sources S1 and S2 separated by a distance L and emitting light of wavelength λ.
1. Understanding the Setup:
- We have two coherent sources S1 and S2 separated by a distance L.
- A screen is placed perpendicular to the line joining the two sources, and it meets the line at point A.
2. Path Difference:
- For any point on the screen, the light waves from S1 and S2 will travel different distances to reach that point.
- The path difference Δr between the two waves arriving at point A can be expressed as:
Δr=r2−r1
where r1 and r2 are the distances from S1 and S2 to point A, respectively.
3. Condition for Constructive Interference:
- Constructive interference occurs when the path difference is an integer multiple of the wavelength:
Δr=nλ(n=0,1,2,…)
- This means that at points where this condition is satisfied, we will observe bright fringes.
4. Condition for Destructive Interference:
- Destructive interference occurs when the path difference is a half-integer multiple of the wavelength:
Δr=(n+12)λ(n=0,1,2,…)
- This means that at points where this condition is satisfied, we will observe dark fringes.
5. Fringe Pattern:
- The interference pattern will consist of alternating bright and dark fringes on the screen.
- Since L is much greater than λ, the fringes will be closely spaced, and the pattern will be approximately linear.
6. Maxima and Minima:
- The point A can be considered as a point of maximum intensity if the path difference Δr at that point satisfies the condition for constructive interference.
- Specifically, if L=nλ, then point A will be a maximum.
Final Conclusion:
- The interference fringes on the screen will be straight lines, and point A will be an intensity maximum if L is an integer multiple of λ.
- We have two coherent sources S1 and S2 separated by a distance L.
- A screen is placed perpendicular to the line joining the two sources, and it meets the line at point A.
- For any point on the screen, the light waves from S1 and S2 will travel different distances to reach that point.
- The path difference Δr between the two waves arriving at point A can be expressed as:
Δr=r2−r1
where r1 and r2 are the distances from S1 and S2 to point A, respectively.
- Constructive interference occurs when the path difference is an integer multiple of the wavelength:
Δr=nλ(n=0,1,2,…)
- This means that at points where this condition is satisfied, we will observe bright fringes.
- Destructive interference occurs when the path difference is a half-integer multiple of the wavelength:
Δr=(n+12)λ(n=0,1,2,…)
- This means that at points where this condition is satisfied, we will observe dark fringes.
- The interference pattern will consist of alternating bright and dark fringes on the screen.
- Since L is much greater than λ, the fringes will be closely spaced, and the pattern will be approximately linear.
- The point A can be considered as a point of maximum intensity if the path difference Δr at that point satisfies the condition for constructive interference.
- Specifically, if L=nλ, then point A will be a maximum.
- The interference fringes on the screen will be straight lines, and point A will be an intensity maximum if L is an integer multiple of λ.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct8videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective11videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
Two coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
 View Solution
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 View Solution
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 View Solution
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .View Solution
.View SolutionThe coherent point sources S1 and S2 vibrating in same phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance from S2 where a minimum of intensity occurs due to interference of waves from the two sources?
View SolutionThe coherent point sources S1 and S2 vibrating in same phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passingh through S2 and perpendicular to the line S1S2. What is the smallest distance from S2 where a minimum of intensity occurs due to interference of waves from the two sources?
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between the sources is 2λ. The smallest distance from S2 on a line passing through S2 and perpendicular to s1s2 where a minimum of intensity occurs is
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View SolutionConsider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
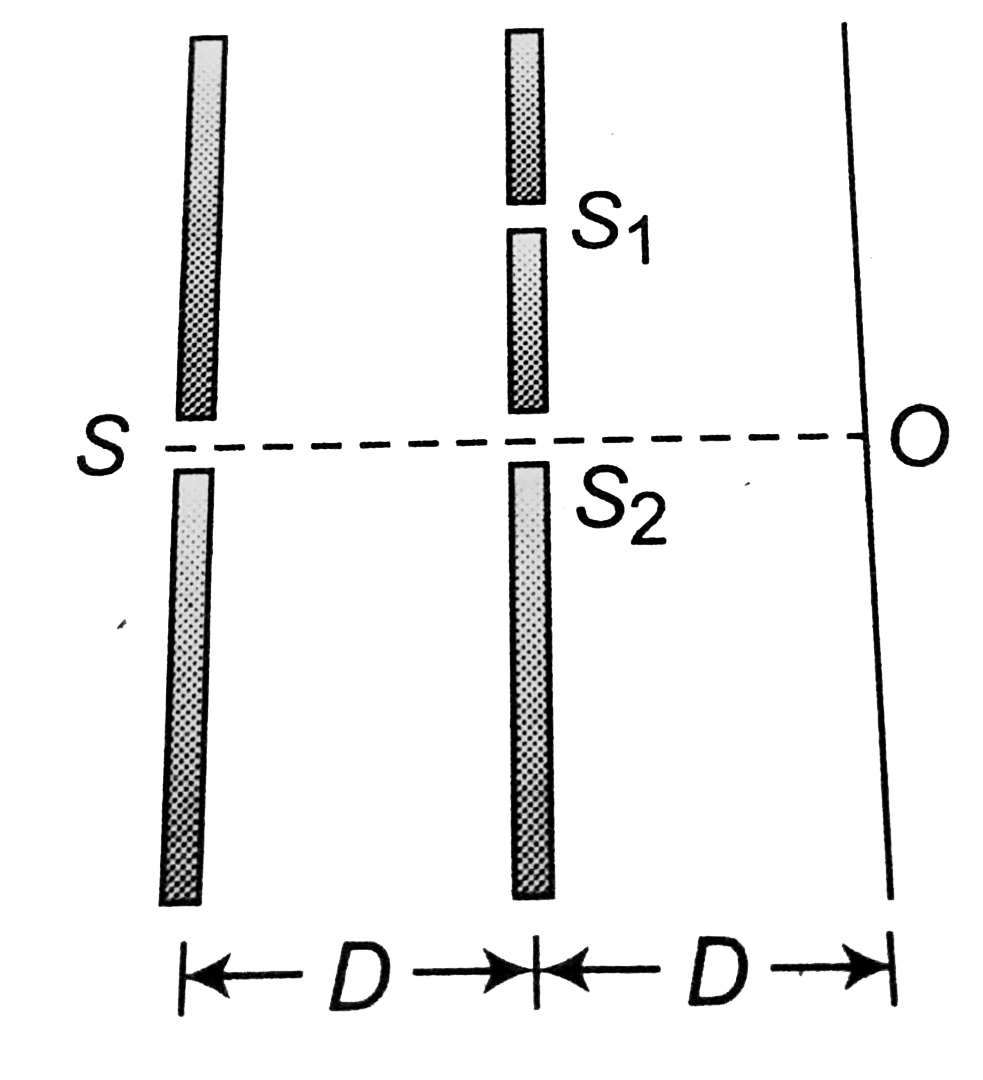
View SolutionTwo ideal slits S1 and S2 are at a distance d apart, and illuninated by light of wavelength λ passing through an ideal source slit S placed on the line through S2 as shown. The distance between the planes of slits and the source slit is D.A screen is held at a distance D from the plane of the slits. The minimum value of d for which there is darkness at O is (d<<D)
 View Solution
View Solution
