Two thin parallel slits are made in on opaque sheet of film when a monochromatic beam of light is shonw through then at normal incidence. The first bright fringes in the transmitted light occur at ±45∘ with the original direction of the ligth beam on a distant screen when the apparatus is in air. When the apparatus is immersed in a liquid, the same bright fringe now occur at ±30∘. The index of refraction of the liquid is
√2
√3
43
32
The correct Answer is:a
To solve the problem, we will use the principles of Young's double-slit experiment and the relationship between the angles of the bright fringes and the refractive index of the medium.
1. Understanding the Setup:
- We have two thin parallel slits and a monochromatic light source. The first bright fringes occur at angles of ±45° when in air and at ±30° when in a liquid.
2. Using the Condition for Bright Fringes:
- The condition for the first bright fringe in Young's double-slit experiment is given by:
dsinθ=nλ
- Here, d is the distance between the slits, θ is the angle of the bright fringe, n is the order of the fringe (for the first bright fringe, n=1), and λ is the wavelength of light.
3. Setting Up the Equations:
- For air (where the first bright fringe occurs at ±45°):
dsin(45∘)=λ
- For the liquid (where the first bright fringe occurs at ±30°):
dsin(30∘)=λ′
- The wavelength in the liquid λ′ is related to the wavelength in air λ by the refractive index μ:
λ′=λμ
4. Relating the Two Conditions:
- From the first condition in air:
dsin(45∘)=λ
- From the second condition in the liquid:
dsin(30∘)=λμ
5. Dividing the Two Equations:
- Dividing the first equation by the second gives:
dsin(45∘)dsin(30∘)=λλμ
- Simplifying this, we have:
sin(45∘)sin(30∘)=μ
6. Calculating the Sines:
- We know:
sin(45∘)=√22,sin(30∘)=12
- Substituting these values:
μ=√2212=√2
7. Conclusion:
- The index of refraction of the liquid is:
μ=√2
- We have two thin parallel slits and a monochromatic light source. The first bright fringes occur at angles of ±45° when in air and at ±30° when in a liquid.
- The condition for the first bright fringe in Young's double-slit experiment is given by:
dsinθ=nλ
- Here, d is the distance between the slits, θ is the angle of the bright fringe, n is the order of the fringe (for the first bright fringe, n=1), and λ is the wavelength of light.
- For air (where the first bright fringe occurs at ±45°):
dsin(45∘)=λ
- For the liquid (where the first bright fringe occurs at ±30°):
dsin(30∘)=λ′
- The wavelength in the liquid λ′ is related to the wavelength in air λ by the refractive index μ:
λ′=λμ
- From the first condition in air:
dsin(45∘)=λ
- From the second condition in the liquid:
dsin(30∘)=λμ
- Dividing the first equation by the second gives:
dsin(45∘)dsin(30∘)=λλμ
- Simplifying this, we have:
sin(45∘)sin(30∘)=μ
- We know:
sin(45∘)=√22,sin(30∘)=12
- Substituting these values:
μ=√2212=√2
- The index of refraction of the liquid is:
μ=√2
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
When entire Young's double slit apparatus is immersed in a liquid the fringe width decreases by 20∘. The refractive index of the liquid is
View SolutionA:When the apparatus of YDSE is brought in a liquid from air, the fringe width decreases.
R: The wavelength of light decreases in the liquid.
View SolutionThe width of a slit is 0.012mm. Monochromatic light is incident on it. The angular position of first bright line is 5.20. The wavelength of the light incident is
View SolutionTwo parallel beams of light of wavelength λ inclined to each other at angle θ(<<1) are incident on a plane at near normal incidence. The fringe width will be :
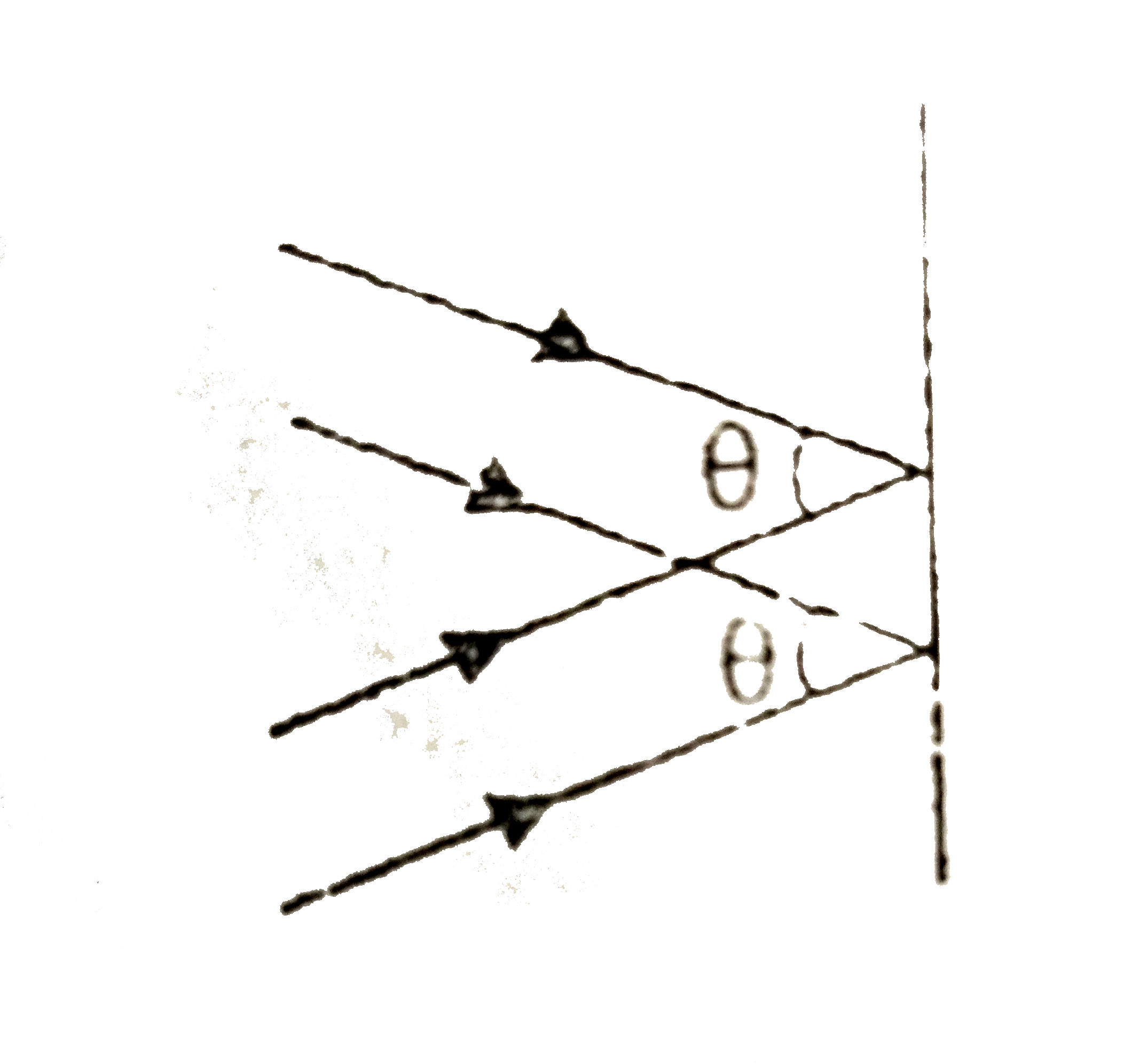
View SolutionA : If the whole apparatus of Young.s experiment is immersed in liquid, the fringe width will decrease.
R : The wavelength of light in water is more than that in air.
View SolutionTwo thin parallel slits that are 0.012 mm apart are illuminated by a laser beam of wavelength 650 nm. On a very large distant screen, the total number of bright fringes including the central fringe and those on both sides of it is
View SolutionA monochromatic beam of light is used for the formation of fringes on a screen by illuminating the two slits in the Young,s double slit interference experiment. When a thin film of mic is interposed in the path of one of the interfering beams
View SolutionIn Young's experiment , the fringe width of the fringes with light of wavelength 6000 Å is 2.0 mm . What will be the fringe width if the entire apparatus is immersed in a liquid of refractive index 1.33 ?
View SolutionHow does the fringe width of interference fringes change, when the whole apparatus of Young's experiment is kept in a liquid of refractive index 1.3 ?
View SolutionA parallel monochromatic beam of light is incident normally on a narrow slit. A diffraction patten is formed on a screen placed perpendicular to the direction of incident beam. At the first maximum of the diffraction pattern the phase difference between the rays coming from the edges of the slit is
View Solution
