The width of a slit is 0.012mm. Monochromatic light is incident on it. The angular position of first bright line is 5.20. The wavelength of the light incident is
6040A0
4026A0
5890A0
7248A0
The correct Answer is:D
To find the wavelength of the monochromatic light incident on a slit, we can use the formula for diffraction at a single slit. The formula for the angular position of the first bright fringe is given by:
dsinθ=(2n+1)λ2
Where:
- d is the width of the slit,
- θ is the angular position of the bright fringe,
- n is the order of the bright fringe (for the first bright fringe, n=1),
- λ is the wavelength of the light.
Step 1: Convert the slit width to meters
Given:
- Width of the slit d=0.012mm
Convert to meters:
d=0.012mm=0.012×10−3m=12×10−6m
Step 2: Identify the angular position and convert to radians if necessary
Given:
- Angular position of the first bright line θ=5.2∘
We can use the sine function directly in degrees:
sin(5.2∘)≈0.0906
Step 3: Substitute values into the formula for wavelength
Using the formula:
λ=2dsinθ2n+1
Substituting n=1:
λ=2×(12×10−6)×0.09062×1+1
Step 4: Calculate the wavelength
Calculate the denominator:
2n+1=2×1+1=3
Now substitute into the equation:
λ=24×10−6×0.09063
Calculating the numerator:
24×10−6×0.0906=2.1744×10−6
Now divide by 3:
λ=2.1744×10−63=0.7248×10−6m
Step 5: Convert the wavelength to angstroms
1 meter = 1010 angstroms, so:
λ=0.7248×10−6m=7248angstroms
Final Answer
The wavelength of the light incident is:
λ=7248angstroms
- d is the width of the slit,
- θ is the angular position of the bright fringe,
- n is the order of the bright fringe (for the first bright fringe, n=1),
- λ is the wavelength of the light.
Given:
- Width of the slit d=0.012mm
d=0.012mm=0.012×10−3m=12×10−6m
Given:
- Angular position of the first bright line θ=5.2∘
sin(5.2∘)≈0.0906
Using the formula:
λ=2dsinθ2n+1
Substituting n=1:
λ=2×(12×10−6)×0.09062×1+1
Calculate the denominator:
2n+1=2×1+1=3
λ=24×10−6×0.09063
24×10−6×0.0906=2.1744×10−6
λ=2.1744×10−63=0.7248×10−6m
1 meter = 1010 angstroms, so:
λ=0.7248×10−6m=7248angstroms
The wavelength of the light incident is:
λ=7248angstroms
Topper's Solved these Questions
- WAVES OPTICSBook:AAKASH SERIESChapter:WAVES OPTICSExercise:EXERCISE -II (POLARISATION)
Explore 10 Videos
- WAVES OPTICSBook:AAKASH SERIESChapter:WAVES OPTICSExercise:EXERCISE -III (DOPPLER EFFECT IN LIGHT, INTERFERENCE)
Explore 25 Videos
- WAVES OPTICSBook:AAKASH SERIESChapter:WAVES OPTICSExercise:EXERCISE -II (INTERFERENCE)
Explore 26 Videos
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-III (Doppler effect :)
Explore 15 Videos
Similar Questions
Light of wavelength 6000Å is incident on a slit of width 0.30 mm. The screen is placed 2 m from the slit. Find (a) the position of the first dark fringe and (b). The width of the central bright fringe.
View SolutionMonochromatic light of wavelength 580 nm is incident on a slit of width 0.30 mm. The screen is 2m from the slit . The width of the central maximum is
View SolutionA ray of light is incident perpendicularly on a glass slab. The angle of incidence is 900.
View SolutionIn the diffration due to single slit experiment, the aperture of the slit is 3 mm. If monochromatic light of wavelength 620 nm in incident normally on the slit, calculate the separation in between the first order minima and the 3rd order maxima on one side of the screen. The distance between the slit and the screen is 1.5 m.
View SolutionFor a parallel beam of monochromatic light of wavelength 'λ' diffraction is produced by a single slit whose width 'a' is of the order of the wavelength of the light. If 'D' is the distance of the screen from the slit, the width of the central maxima will be
View SolutionIn Young's double slit experiment ,momochromatic light of wavelength 630nm illuminates the pair of slits and produces an interface pattern pattern in which two consecutive bright frings are separated by 8.1mm. Another source of monochromatic light produce the interface pattern in which the two consecutive bright fringes are seperated by 7.2mm, find the wavelength of light from the second sources . What is the effect to on the interference fringes if the monochromatic sources is replaced by a source of white light ?
View SolutionIn a single slit differaction pattern a monochromatic light of wavelength 500nm is used if angular position of the point where waves interfere from slit is 10−3 radians from line of central maxima. If width of the slit is 500μm, then order of minima obtained on screen will be
View SolutionIn Young's double slit experiment parallel monochromatic light is incident on both the slits at an angle as shown in the figure. To obtain the central maxima at on the screen we can
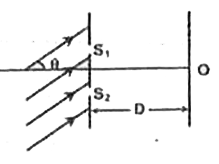
View SolutionMonochromatic light of wavelength 198 nm is incident on the surface of a metal, whose work function is 2.5 eV. Calculate the stopping potential.
View SolutionLight of wavelength 6000Å is incident on a slit of width 0.30 mm. The screen is placed 2 m from the slit. Find (a) the position of the first dark fringe and (b). The width of the central bright fringe.
View Solution

