In Young's double-slit experiment, let A and B be the two slit. A thin film of thickness t and refractive index μ is placed in front of A. Let β= fringe width. Then the central maxima will shift
toward A
toward B
by t(μ−1)βλ
by μtβλ
The correct Answer is:a.,c
To solve the problem of how much the central maxima will shift in Young's double-slit experiment when a thin film is placed in front of one of the slits, we can follow these steps:
1. Understanding the Setup:
In Young's double-slit experiment, we have two slits A and B. A thin film of thickness t and refractive index μ is placed in front of slit A.
2. Path Difference Calculation:
The introduction of the thin film changes the optical path length for light passing through slit A. The optical path length through the film is given by:
Optical Path Length=μt
The geometrical path length is simply t. Therefore, the path difference Δ introduced by the thin film is:
Δ=Optical Path Length−Geometrical Path Length=μt−t=t(μ−1)
3. Relating Path Difference to Fringe Shift:
In Young's experiment, the path difference that leads to a shift in the position of the central maxima is given by:
Δ=XDd
where X is the shift in the position of the central maxima, D is the distance from the slits to the screen, and d is the distance between the slits.
4. Setting the Equations Equal:
Equating the two expressions for path difference, we have:
XDd=t(μ−1)
5. Solving for the Shift X:
Rearranging the equation to solve for X:
X=t(μ−1)dD
6. Relating to Fringe Width:
The fringe width β is given by:
β=λDd
From this, we can express dD in terms of fringe width:
dD=βλ
7. Substituting Back:
Substituting dD into the expression for X:
X=t(μ−1)(βλ)
8. Final Expression:
Thus, the shift of the central maxima is given by:
X=t(μ−1)βλ
Conclusion:
The central maxima will shift by t(μ−1)βλ towards slit A.
In Young's double-slit experiment, we have two slits A and B. A thin film of thickness t and refractive index μ is placed in front of slit A.
The introduction of the thin film changes the optical path length for light passing through slit A. The optical path length through the film is given by:
Optical Path Length=μt
The geometrical path length is simply t. Therefore, the path difference Δ introduced by the thin film is:
Δ=Optical Path Length−Geometrical Path Length=μt−t=t(μ−1)
In Young's experiment, the path difference that leads to a shift in the position of the central maxima is given by:
Δ=XDd
where X is the shift in the position of the central maxima, D is the distance from the slits to the screen, and d is the distance between the slits.
Equating the two expressions for path difference, we have:
XDd=t(μ−1)
Rearranging the equation to solve for X:
X=t(μ−1)dD
The fringe width β is given by:
β=λDd
From this, we can express dD in terms of fringe width:
dD=βλ
Substituting dD into the expression for X:
X=t(μ−1)(βλ)
Thus, the shift of the central maxima is given by:
X=t(μ−1)βλ
The central maxima will shift by t(μ−1)βλ towards slit A.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
The figure shows a Young's double slit experimental setup. It is observed that when a thin transparent sheet of thickness t and refractive index μ is put front of one of the slits, the central maximum gets shifted by a distance equal to n fringe widths. If the wavelength of light used is λ, t will be :
View SolutionIn YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
View SolutionIn a Young's double slit experimental arrangement shown here, if a mica sheet of thickness t and refractive indec μ is placed in front of the slit S1, then the path difference (S1P−S2P) is

View SolutionIn Young's double slit experiment, the distance between two slits is made three times then the fringe width will becomes
View SolutionA double slit experiment is performed with light of wavelength 500nm. A thin film of thickness 2μm and refractive index 1.5 is introduced in the path of the upper beam. The location of the central maximum will
View SolutionIn YDSE, let A and B be two slits. Films of thickness tA and tB and refractive μA and μB are placed in front of A and B, respectively. If μAtA=μAtB, then the central maxima will
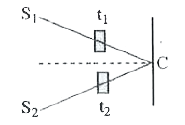
View SolutionIn Young's double slit experiment S1 and S2 are two slits. Films of thickness t1 and t2 and refractive indices μ1 and μ2 are placed in front of S1 and S2 respectively. If μ1t1=μ2t2, then the central maximum will :
View SolutionIn young's double slit experiment, fringe order is represented by m, then fringe width is
View SolutionIn a doulble slit experiment when a thin film of thickness t having refractive index μ is introduced in from of one of the slits, the maximum at the centre of the fringe pattern shifts by one width. The value of t is (λ is the wavelength of the light used)
View SolutionA call is connected between the point A and C of a circular conductor ABCD of centre O with angle AOC=60∘ . If B1 and B2 are the magnitudes of the magnetic field at O due ti the currents In ADC respectively, the ratio B1B2 is

View Solution
