Assertion: Two coherent sources S1andS2 are placed in front of a screen as shown in figure. At point P, 10th order maxima is obtained. Then , 11th order maxima will be obtained above P.
Reason: For 11th order maxima path difference should be more.
(a)If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
(b)If both Assertion and Reason are true and the Reason is not the correct explanation of the Assertion.
(c) If Assertion is true, but the Reason is false.
(d) If Assertion is false, but the Reason is true.
The correct Answer is:D
To solve the problem, we need to analyze both the assertion and the reason provided in the question.
Step 1: Understanding the Assertion
The assertion states that at point P, the 10th order maxima is obtained, and it claims that the 11th order maxima will be obtained above point P.
Step 2: Analyzing the Path Difference
In a double-slit interference pattern, the position of the maxima on the screen is determined by the path difference between the light waves coming from the two coherent sources S1 and S2. The condition for maxima (bright fringes) is given by:
Δx=nλ
where n is the order of the maxima, and λ is the wavelength of the light.
Step 3: Determining the Position of Maxima
For the 10th order maxima (n=10), the path difference at point P is:
Δx10=10λ
For the 11th order maxima (n=11), the path difference would be:
Δx11=11λ
Step 4: Conclusion on the Position of Maxima
Since the path difference increases with the order of the maxima, the 11th order maxima will be located at a position where the path difference is greater than that of the 10th order maxima. However, in a typical interference pattern, as we move further away from the central maximum, the positions of higher order maxima (like the 11th) will be found further down the screen, not above point P.
Thus, the assertion that the 11th order maxima will be obtained above P is false.
Step 5: Analyzing the Reason
The reason states that for the 11th order maxima, the path difference should be more. This is indeed true, as we established that:
Δx11>Δx10
Final Conclusion
- The assertion is false because the 11th order maxima will not be above point P.
- The reason is true because the path difference for the 11th order maxima is indeed greater than that for the 10th order maxima.
Answer
Thus, the final answer is that the assertion is false, and the reason is true.
---
The assertion states that at point P, the 10th order maxima is obtained, and it claims that the 11th order maxima will be obtained above point P.
In a double-slit interference pattern, the position of the maxima on the screen is determined by the path difference between the light waves coming from the two coherent sources S1 and S2. The condition for maxima (bright fringes) is given by:
Δx=nλ
where n is the order of the maxima, and λ is the wavelength of the light.
For the 10th order maxima (n=10), the path difference at point P is:
Δx10=10λ
For the 11th order maxima (n=11), the path difference would be:
Δx11=11λ
Since the path difference increases with the order of the maxima, the 11th order maxima will be located at a position where the path difference is greater than that of the 10th order maxima. However, in a typical interference pattern, as we move further away from the central maximum, the positions of higher order maxima (like the 11th) will be found further down the screen, not above point P.
The reason states that for the 11th order maxima, the path difference should be more. This is indeed true, as we established that:
Δx11>Δx10
- The assertion is false because the 11th order maxima will not be above point P.
- The reason is true because the path difference for the 11th order maxima is indeed greater than that for the 10th order maxima.
Thus, the final answer is that the assertion is false, and the reason is true.
Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 1 Objective
11 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Objective question
2 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Exercise 32.2
6 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
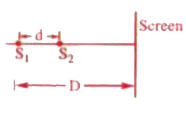
Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View SolutionTwo coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
View SolutionAssertion: In the figure shown, zero order maxima will lie above point O.
Reason: Zero order maxima normally means a point where path difference is zero.
View SolutionAssertion: In the YDSE apparatus shown in figure dltltD and dλ=4, then second order maxima will be obtained at θ=30∘
Reason: Total seven maxima will be obtained on screen.
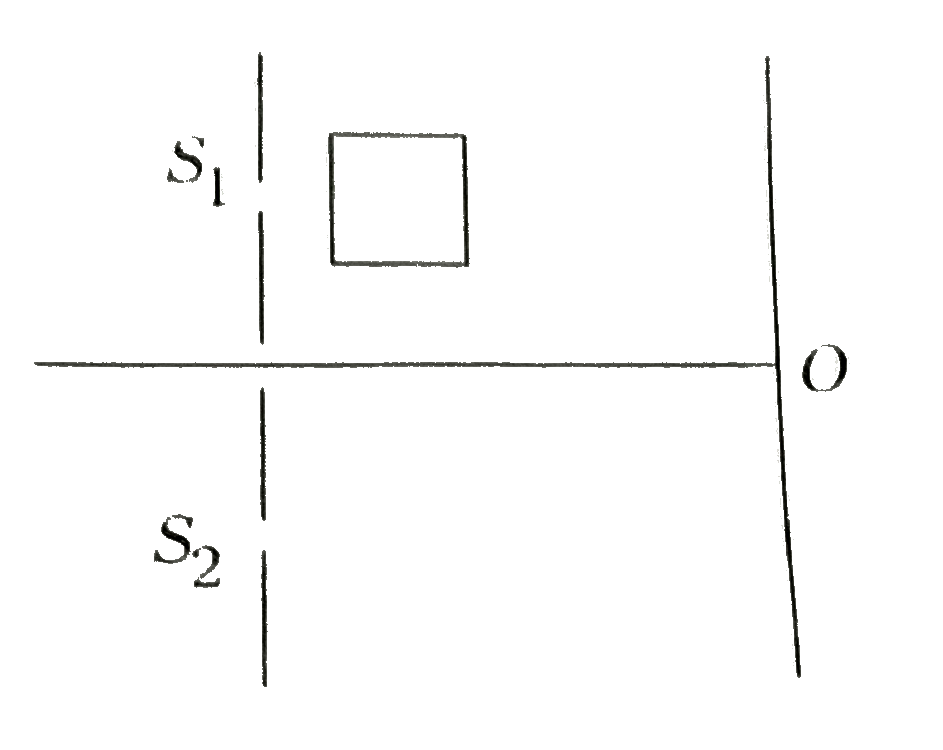
View SolutionAssertion In the YDSE set up shown in figure a glass slab is inserted in front of the slit S1 as shown in figure Then zero order maxima (where path difference =0) will lie above point O.
Reason Glass slab will produce an extra path difference in the path of the ray passing through S1
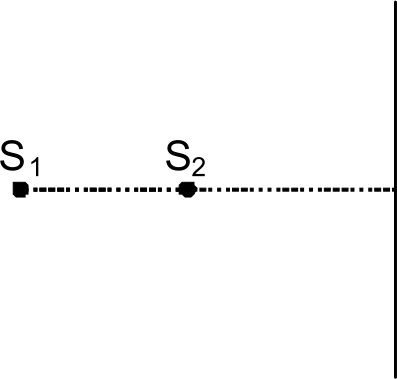
View SolutionStatement I: Two point coherent sources of light S1 and S2 are placed on a line as shown in figure. P and Q are two points on that line. If at point P maximum intensity is observed, then maximum intensity should also be observed at Q.

Statement II: In figure the distance |S1P−S2P| is equal to distance |S1Q−S2Q|.
View SolutionTwo coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 is
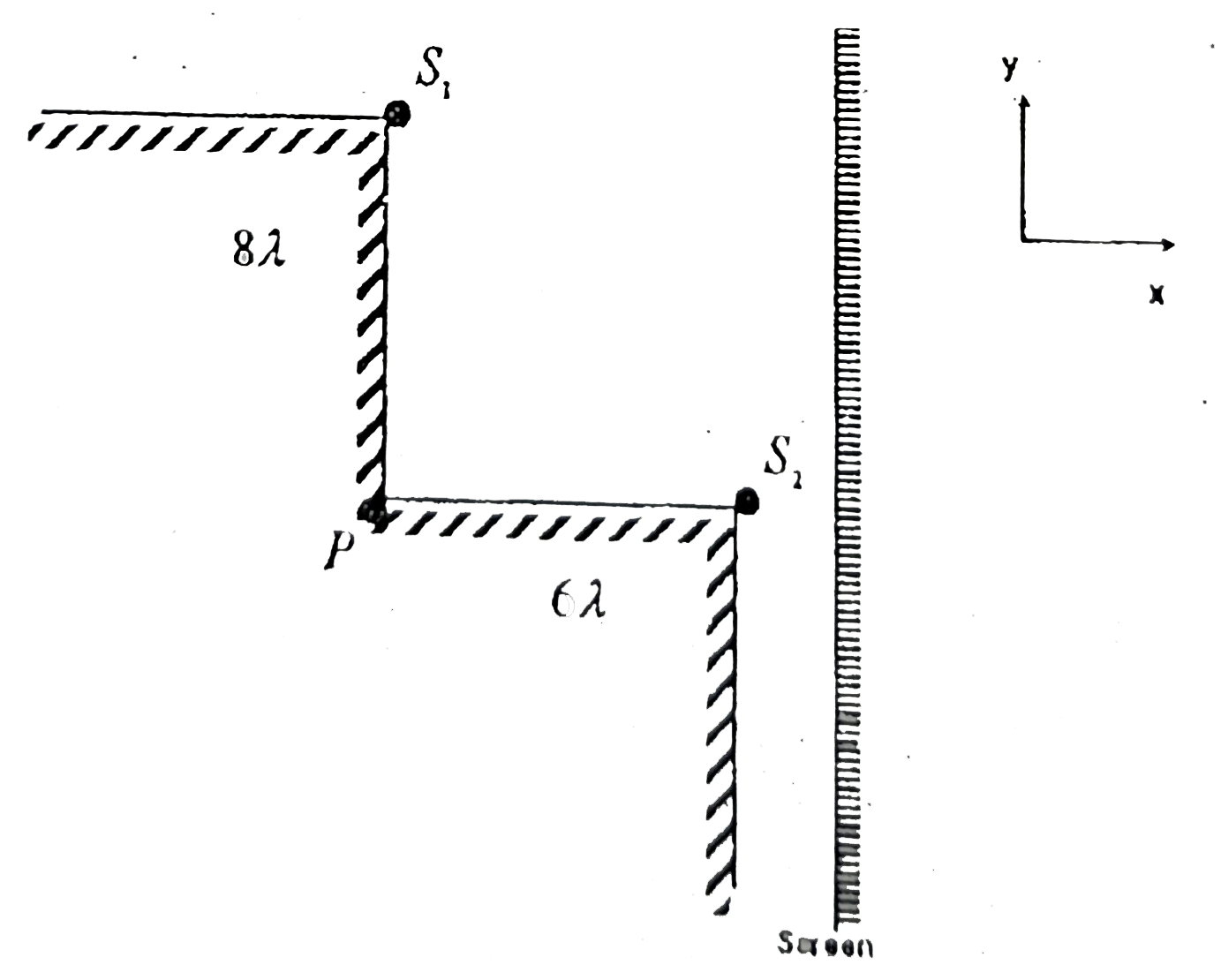
View SolutionTwo coherent sources S1 and S2 are kept on the edges of a step as shown in the figure. An infinitely long screen is placed on the right side of sources and lies at along y−z plane. Calculate total no. of maximas observed on the screen. PS1=8λ and PS2=6λ. Where λ is wavelength of light used. (There is no reflection from steps)
View SolutionAssertion: A monochromatic source of light is placed above a plane mirror as shown in figure. Fringes will be obtained at all points above O but not below it on the screen.
Reason: All reflected rays will suffer a phase difference of π.
View Solution
