In YDSE arrangement as shown in the figure, fringes are seen on screen using monochromatic source S having wavelength 3000Å (in the air). S1andS2 are two slits separated by d = 1 mm and D = 1 m. Left of slits s1ands2 medium of refractive index n1=2 is present and to the right of S1andS2 medium of n2=32, is present. A thin slab of thickness 't' is placed in front of S1. The refractive index of n3 of the slab varies with distance from it's starting face as shown in figure.
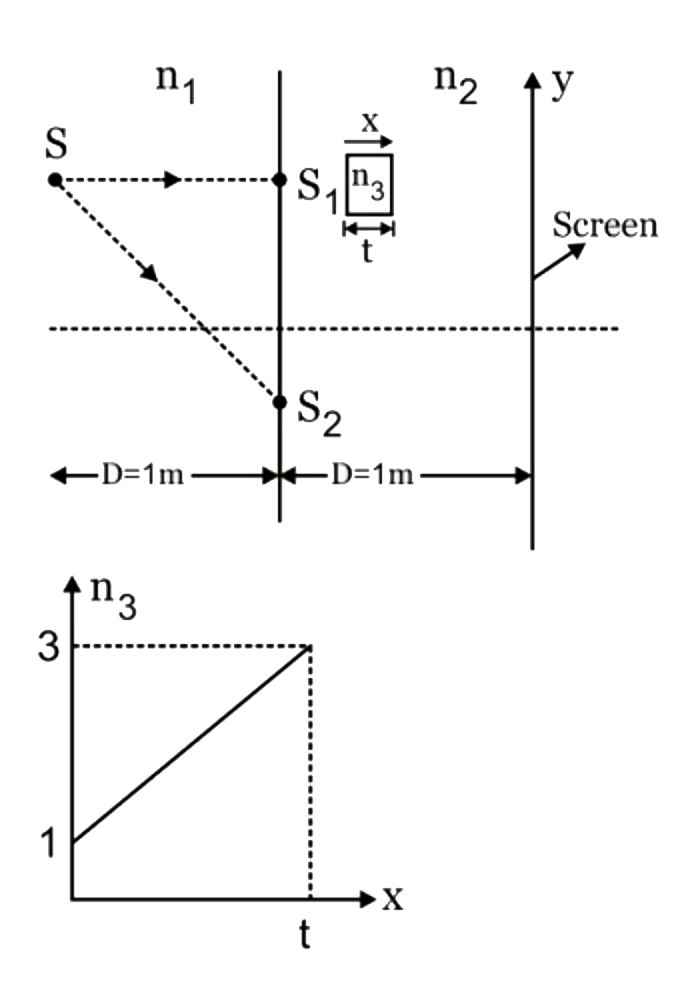
In order of get central maxima at the centre of the screen, the thickness of the slab (in μm) required is :
1μm
2μm
0.5μm
1.5μm
Path difference
Δx=n1SS2+n2S2P−[(n1SS1+n2S1P)−∫t0(n3−n2)dx]
=n1(SS2−SS1)+n2(S2P−S1P)−∫t0n3dx+n_(2)t
In order to get central maxima at centre of screen
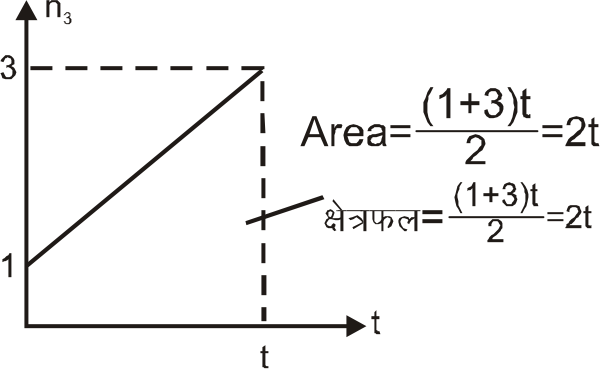
O=2×(1×10−3)22×1+0−2t+3t2
0.5t=1μm
t=2μm
Topper's Solved these Questions
Similar Questions
In YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S1and S2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S1 and S2 medium of refractive index n1=2 is present and to the right of S1 and S2 medium of n2=32, is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of n3 of the slab varies with distance from it's starting face as shown in figure.

In order to get central maxima at the centre of screen, the thickness of slab required is :
View SolutionIn Young's double slit experiment S1 and S2 are two slits. Films of thickness t1 and t2 and refractive indices μ1 and μ2 are placed in front of S1 and S2 respectively. If μ1t1=μ2t2, then the central maximum will :
View Solution
Knowledge Check
SN1 and SN2 reactions are
ABoth stereospecificBBoth stereoselectiveCStereoselective and stereospecific respectivelyDStereospecific and stereoselective respectively
Two coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
View Solution_S01_025_Q01.png)
In Young's double slit experiment the slits, S1&S2 are illuminated by a parallel beam of light of wavelength 4000 Å from the medium of refractive index n1=1.2 A thin film of thickness 1.2 μm and refractive index n=1.5 is placed infrom of S1 perpedicular to path of light. the refractive index of medium between plane of slits & screen is n2=1.4 if the light coming from the film and S1&S2 have equal intensities I then intensity at geometrical centre of the screen O is
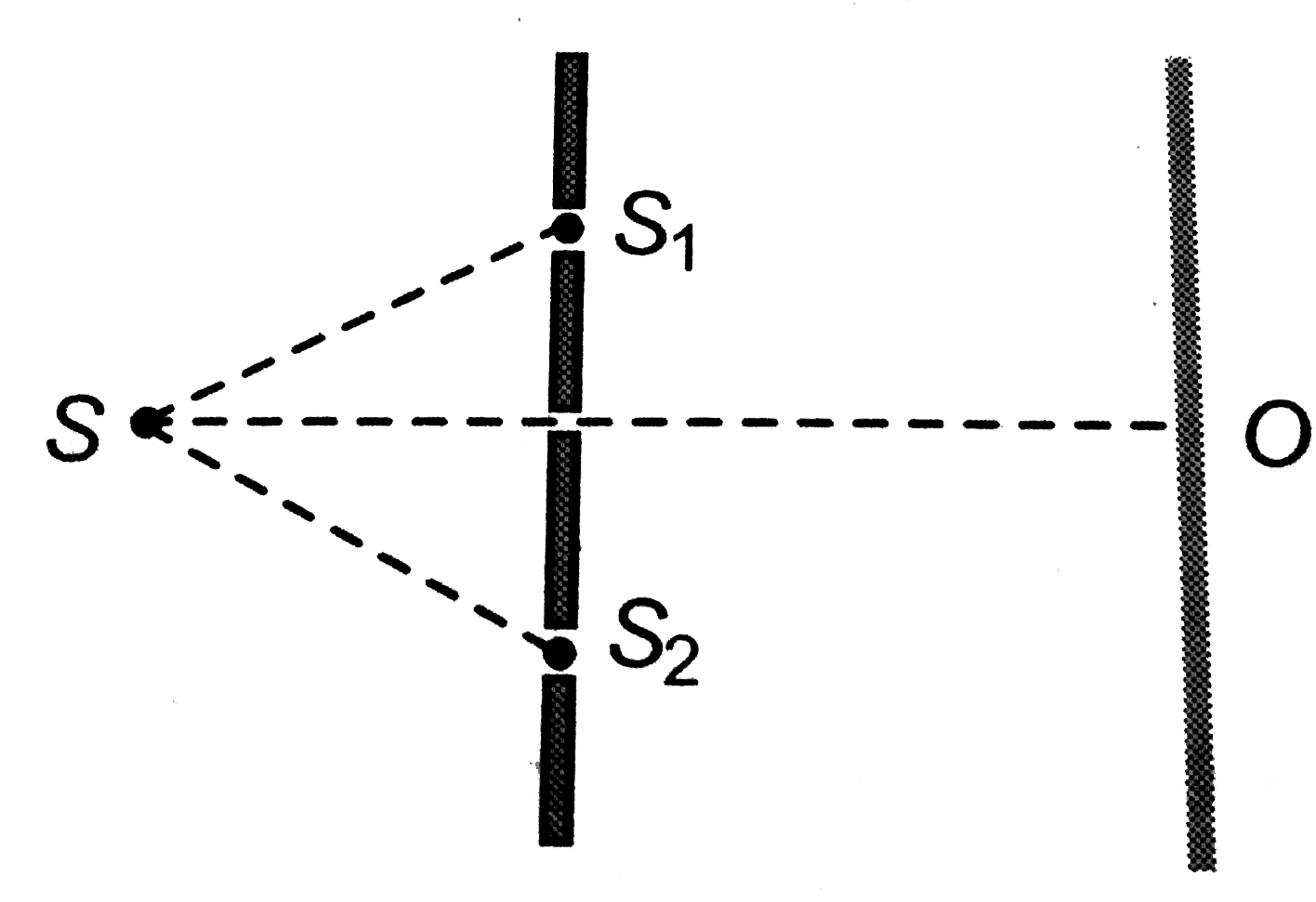
View SolutionIn the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then
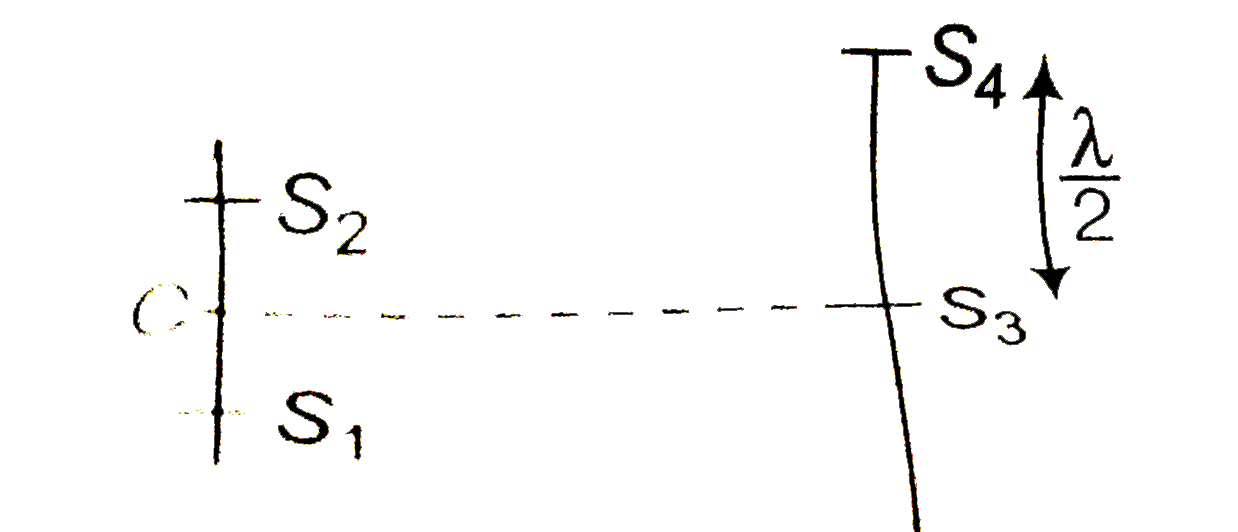
View SolutionIn the given figure ,C is middle point of line S1S2.A monochromatic light of wavelength γ is incident on slits.The ratio of intensites of S3andS4 is
View SolutionTwo monochromatic coherent point sources S1 and S2 are separated by a distance L. Each sources emits light of wavelength λ, where L>>λ. The line S1S2 when extended meets a screen perpendicular to it at point A. Then
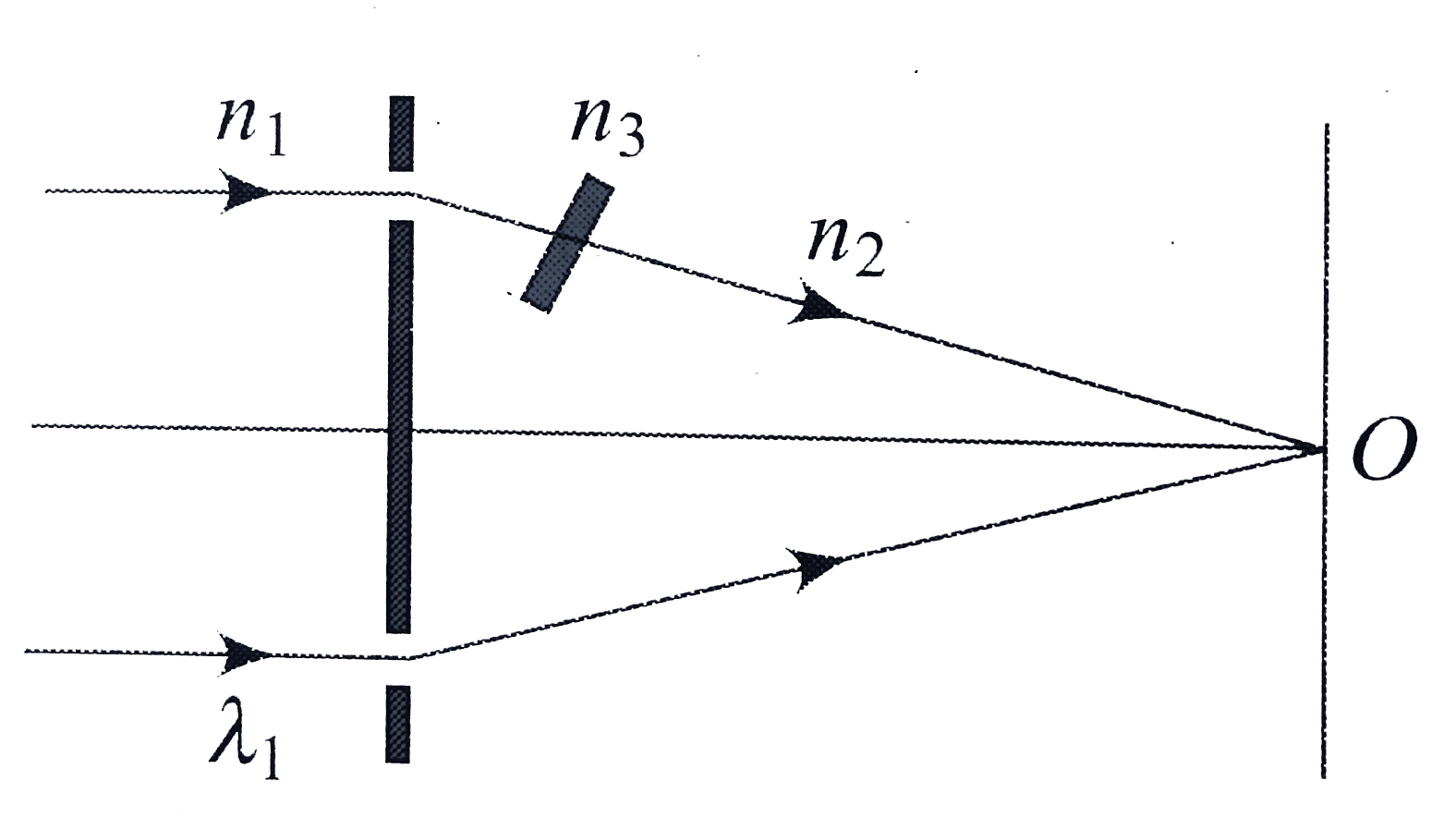
View SolutionIn YDSE shown in figure a parallel beam of light is incident on the slits from a medium of refractive index n1. The wavelength of light in this medium is λ1. A transparent slab of thickness t and refractive index n3 is put in front of one slit. The medium between the screen and the plane of the slits is n2. The phase difference between the light waves reaching point O (symmetrical, relative to the slits) is
View SolutionIn a modified YDSE, sources S is kept in front of slit S1. Find the phase difference at point O that is equidistant from slits S1 and S2 and point P that is in front of slit S1 in the following situations.
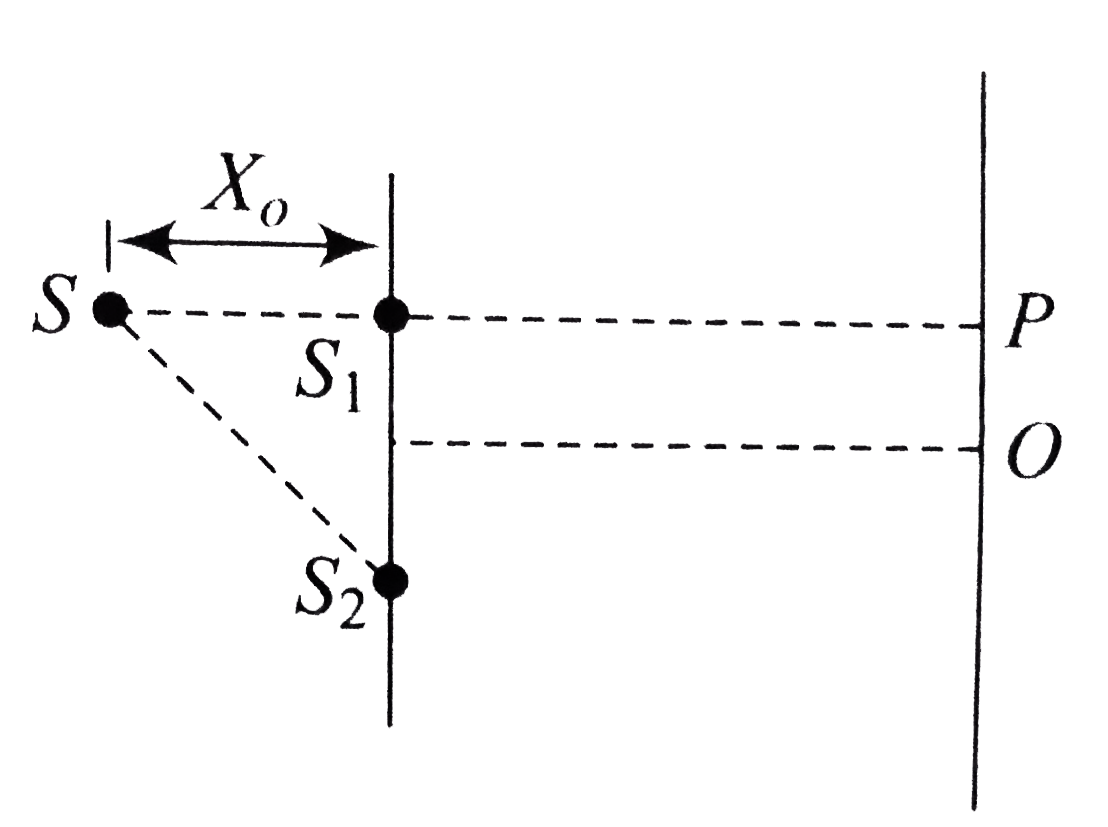
A liquid of refractive index μ is filled between the screen and slits.
View Solution
