A block of dimensions lxtxh and uniform density rests on a rough floor. Wind blowing with speed V and of density falls perpendicularly on one face of dimension lxh of the block as shown in figure. Assuming that air is stopped when it strikes the wall and there is sufficient friction on the ground so that the block does not slide, the minimum speed V so that the block topples is :
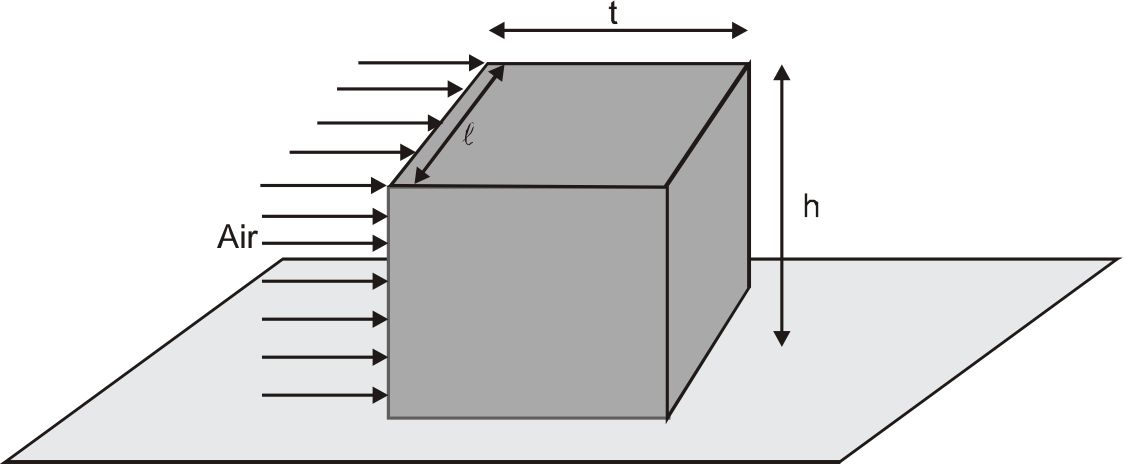
None of these
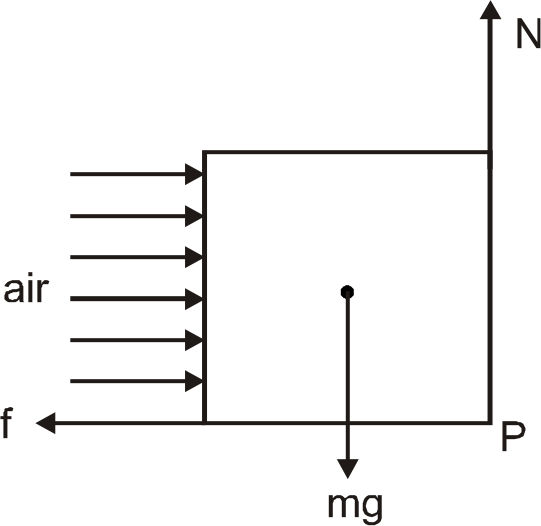
Total torque of air about point P is
for toppling
Topper's Solved these Questions
Similar Questions
In the figure shown, the minimum force F to be applied perpendicular to the incline so that the block does not slide is
 View Solution
View SolutionA cubical block of edge length 1 m and density 800 kg m−3 rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown in figure. If the coefficient of friction is sufficiently large so that the block does not slide bofore toppling, then the minimum value of F to topple the block is [Take g = 10 ms−2]
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cubical box of side L rests on a rough horizontal surface with coefficient of friction p. A horizontal force F is a applied on the block as shown in Fig. 15.4.6. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 AinfinitesimalBmg/4Cmg/2Dmg (−1μ)
AinfinitesimalBmg/4Cmg/2Dmg (−1μ)
A cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?
 View Solution
View SolutionFind the minimum acceleration of the wedge, so that the block is under free fall (assume all surfaces tivate v are smooth).
 View Solution
View SolutionA system is as shown in the figure. All speeds shown are with respect to ground. Then the speed of Block B with respect to ground is :
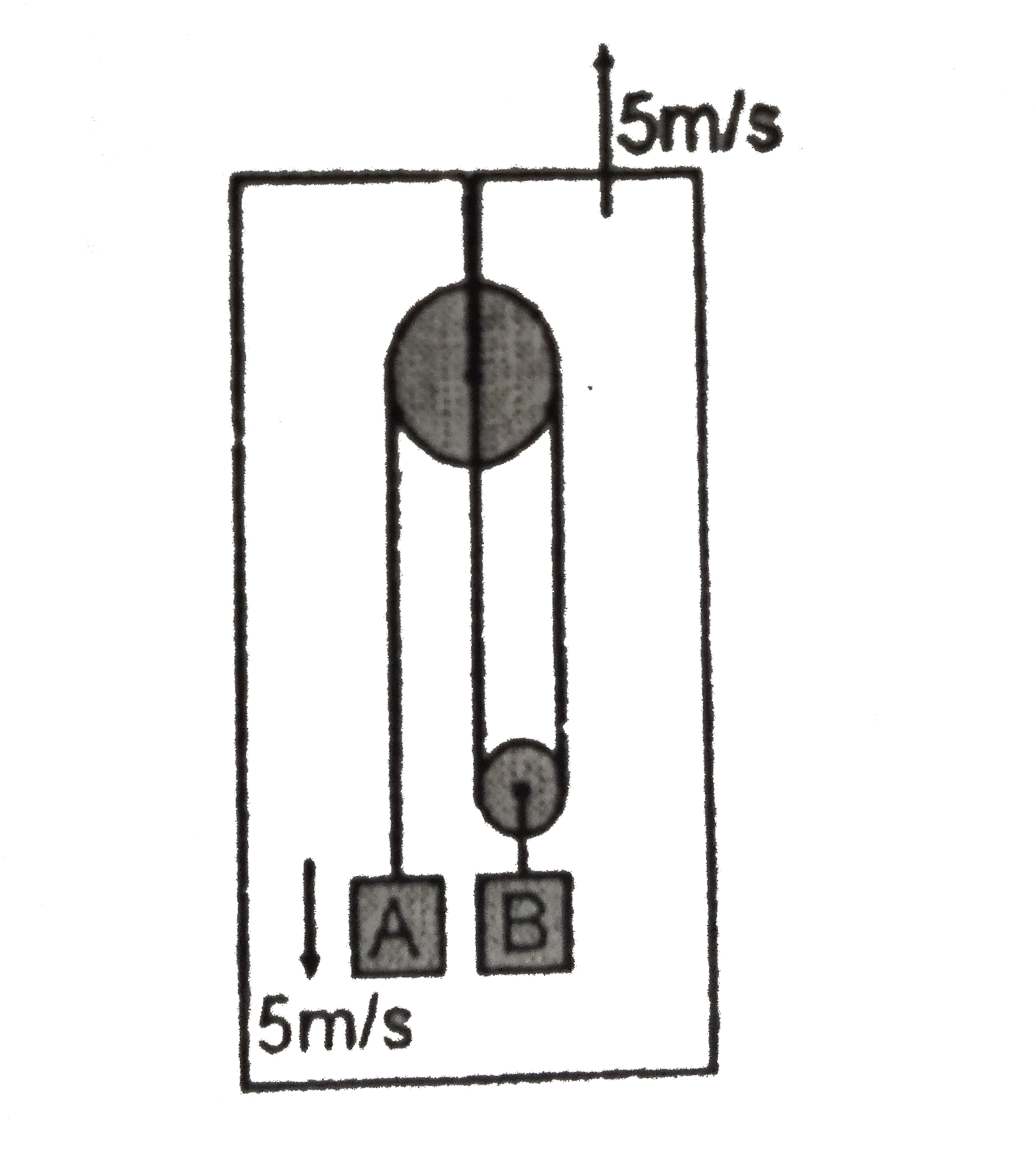 View Solution
View SolutionA block of mass m kept on rough horizontal turn table at a distance x from the centre. If the coefficient of friction between the table and block is μ then maximum speed of point P on turn table so that the block does not slip is
 View Solution
View Solution
Consider the figure shown here of a moving cart C. if the coefficient of friction between the block A and the cart is μ, then calculate the minimum acceleration a of the cart C so that the block A does not fall.View SolutionA block A of mass M rests on a wedge B of mass 2M and inclination θ. There is sufficient friction between A and B so that A does not slip on B. If there is no friction between B and ground, the compression in spring is
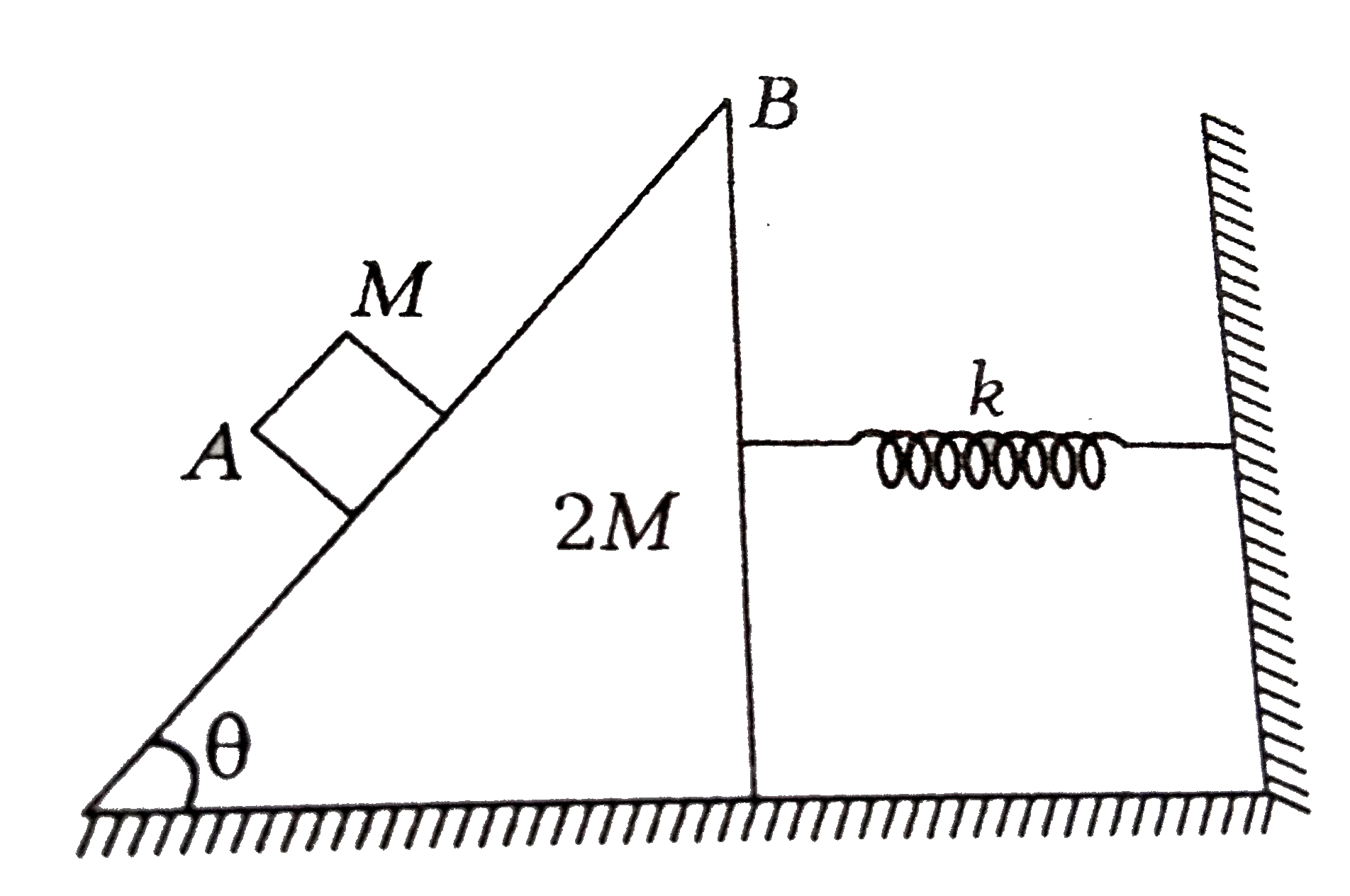 View Solution
View SolutionA block A of mass M rests on a wedge B of mass 2M and inclination θ. There is sufficient friction between A and B so that A does not slip on B. If there is no friction between B and ground, the compression in spring is
 View Solution
View Solution
