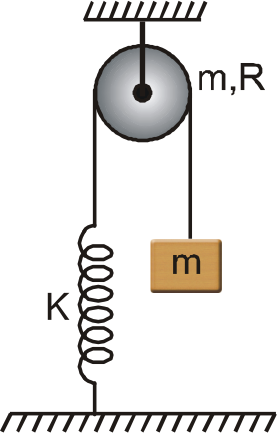
A uniform disc of mass m and radius R is free to rotate about its fixed horizontal axis without friction. There is sufficient friction between the inextensible light string and disc to prevent slipping of string over disc. At the shown instant extension in light spring is 3mgK, where m is mass of block, g is acceleration due to gravity and K is spring constant. Then select the correct alternative(s).
Acceleration of block just after it is released is 4g3
Tension in the string continuously increases till extension in the spring reaches maximum value.
Acceleration of the block just after releases 34g
Angular acceleration of disc just after release is 4g3R
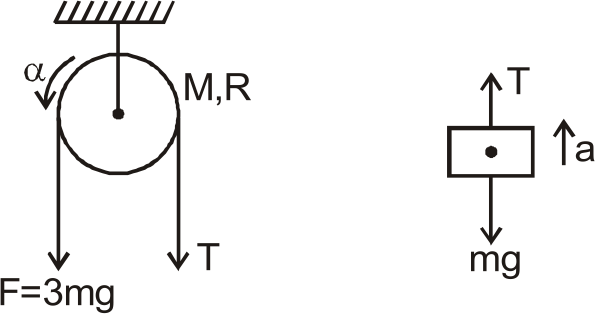
For disc, from torque equation
3mgR−TR=mR22α.....(1)
By application of Newton's second law on block we get,
T−mg=ma.....(2)
where a=Rα....(3)
solving a=4g3
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased, then
View SolutionA solid uniform disc of mass m rols without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:

View SolutionA uniform disc of mass m and radius R is free to rotate about its fixed horizontal axis without friction. There is sufficient friction between the inextensible light string and disc to prevent slipping of string over disc. At the shown instant extension in light spring is (3 mg)/K , where m is mass of block, g is acceleration due to gravity and K is spring constant. Then select the correct alternative(s).
View SolutionIn the figure A and B are two blocks of mass 4kg and 2kg respectively attached to the two ends of light string passing overa disc C of mass 40kg and radius 0.1m. The disc is free to rotate about a fixed horizontal the string does not string does not slip over the disc. Find.
(i) The linear acceleration of mass B.
(ii) the number of revolutions made by the disc at the end of 10sec. from the start.
(iii) the tension in teh string segment supporting the block A.
 .
.
View SolutionA uniform disc of mass M and radius R is rotating freely about its central vertical axis with angular speed w0. Another disc of mass m and radius r is free to rotate about a horizontal rod AB. Length of the rod AB isL(<R) and its end A is rigidly attached to the vertical axis of the first disc. The disc of mass m, initially at rest, is placed gently on the disc of mass M as shown in figure. Find the time after which the slipping between the two discs will cease. Assume that normal reaction between the two discs is equal to mg. Coefficient of friction between the two discs is μ.

View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc. Acceleration of the plank is
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc. Force of friction between the disc and the plank is
View SolutionPassage VIII A disc of mass m and radius R is attached with a spring of force contant k at its center as shown in figure. At x-0, spring is unstretched. The disc is moved to x=A and then released. There is no slipping between disc and ground. Let f be the force of friction on the disc from the ground.

f versus t (time) graph will be as
View SolutionA uniform disc of mass M, radius R is attached to a frictionless horizontal axis. Its rim is wound with a light string and a tension T is applied to it, the angular acceleration will be?
View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View SolutionA disc of mass m and radius R is placed over placed over of mass m. There is sufficient friction between disc & plank to prevent slipping. A force F is applied at centre of disc then
View SolutionA solid uniform disc of mass m rols without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
View SolutionA solid uniform disc of mass m rolls without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank is
View Solution