A uniform ring having mass m, radius R, cross section area of the wire A and young’s modulus Y is rotating with an angular speed ω(ω is small) on a smooth horizontal surface. Which of the following options is correct :
Tension in the wire is mRω22π
Change in length of the wire is mR2ω22A.Y
Change in radius of the ring is mR2ω22πA.Y
elastic potential energy stored is 14π(m2ω4R3A.Y)
To solve the problem regarding the uniform ring rotating on a smooth horizontal surface, we need to analyze the forces acting on the ring and the effects of its rotation.
1. Understanding the System:
- We have a uniform ring with mass m and radius R.
- The ring has a cross-sectional area A and a Young's modulus Y.
- The ring is rotating with an angular speed ω.
2. Centrifugal Force:
- When the ring rotates, it experiences a centrifugal force due to its rotation. The centrifugal force Fc acting on any small element of the ring can be expressed as:
Fc=m⋅ω2⋅R
- This force tends to stretch the ring outward.
3. Stress in the Ring:
- The stress σ in the material of the ring due to the centrifugal force can be calculated using the formula for stress:
σ=FA
- Here, F is the force acting on the cross-sectional area A.
4. Calculating the Force:
- The total force F acting on the ring due to the centrifugal effect can be approximated as the total centrifugal force acting on the entire mass of the ring:
F=m⋅ω2⋅R
- Therefore, the stress in the ring becomes:
σ=m⋅ω2⋅RA
5. Using Young's Modulus:
- Young's modulus Y relates stress and strain in the material:
Y=σϵ
- Where ϵ is the strain. Rearranging gives us:
ϵ=σY
- Substituting the expression for stress:
ϵ=m⋅ω2⋅RA⋅Y
6. Conclusion:
- The strain in the ring due to its rotation can be expressed as:
ϵ=m⋅ω2⋅RA⋅Y
- This equation shows how the parameters of the ring (mass, radius, cross-sectional area, Young's modulus) and the angular speed affect the strain in the ring.
- We have a uniform ring with mass m and radius R.
- The ring has a cross-sectional area A and a Young's modulus Y.
- The ring is rotating with an angular speed ω.
- When the ring rotates, it experiences a centrifugal force due to its rotation. The centrifugal force Fc acting on any small element of the ring can be expressed as:
Fc=m⋅ω2⋅R
- This force tends to stretch the ring outward.
- The stress σ in the material of the ring due to the centrifugal force can be calculated using the formula for stress:
σ=FA
- Here, F is the force acting on the cross-sectional area A.
- The total force F acting on the ring due to the centrifugal effect can be approximated as the total centrifugal force acting on the entire mass of the ring:
F=m⋅ω2⋅R
- Therefore, the stress in the ring becomes:
σ=m⋅ω2⋅RA
- Young's modulus Y relates stress and strain in the material:
Y=σϵ
- Where ϵ is the strain. Rearranging gives us:
ϵ=σY
- Substituting the expression for stress:
ϵ=m⋅ω2⋅RA⋅Y
- The strain in the ring due to its rotation can be expressed as:
ϵ=m⋅ω2⋅RA⋅Y
- This equation shows how the parameters of the ring (mass, radius, cross-sectional area, Young's modulus) and the angular speed affect the strain in the ring.
Topper's Solved these Questions
Similar Questions
A disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View Solution
Knowledge Check
A uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity omega in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
Amω2L2AYBmω2L22AYCmω2L23AYD2mω2L2AYA solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
A smooth uniform, string of natural length l, cross-sectional area A and Young’s modulus Y is pulled along its length by a force F on a horizontal surface. Find the elastic potential energy stored in the string.
View SolutionA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View SolutionTwo cylindrical vessels, each having length 10m and area of cross-sectional area of 1m2, are filled with water and rotated with angular speed ω=20rad/s. Then, which of the following statement is correct ?
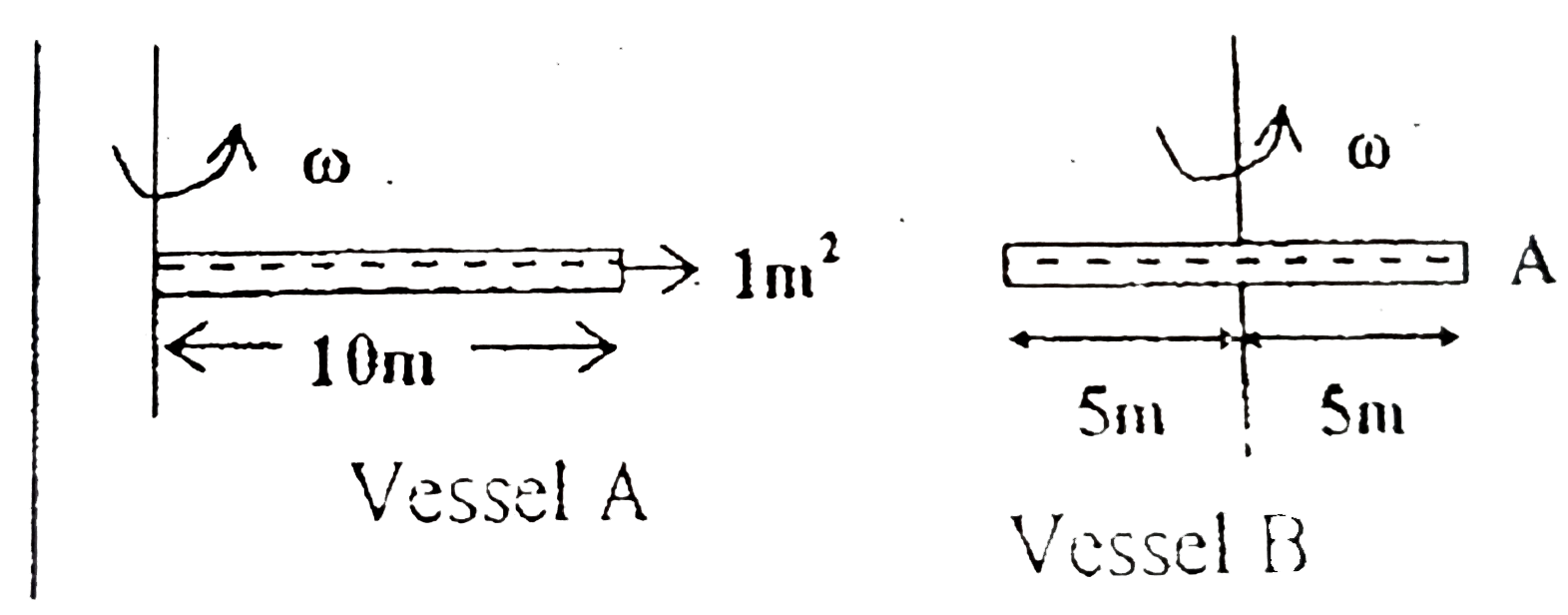
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(i)Current produced due to motion of ring
View Solution

