A disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
12MR2ω
MR2ω
32MR2ω
2MR2ω
The correct Answer is:C
To find the magnitude of the angular momentum of a disc of mass M and radius R rolling with an angular speed ω about the origin, we can follow these steps:
Step 1: Understand the Concept of Angular Momentum
Angular momentum L of a rotating body can be expressed as:
L=Iω
where I is the moment of inertia of the body and ω is the angular speed.
Step 2: Calculate the Moment of Inertia
For a solid disc about its center of mass, the moment of inertia Icm is given by:
Icm=12MR2
Step 3: Apply the Parallel Axis Theorem
Since we need the moment of inertia about the origin (which is a distance R away from the center of the disc), we will use the Parallel Axis Theorem. The theorem states:
I=Icm+Md2
where d is the distance from the center of mass to the new axis (in this case, d=R). Therefore, we have:
I=12MR2+MR2
I=12MR2+22MR2=32MR2
Step 4: Substitute into the Angular Momentum Formula
Now that we have the moment of inertia about the origin, we can substitute it into the angular momentum formula:
L=Iω=(32MR2)ω
Step 5: Final Expression for Angular Momentum
Thus, the magnitude of the angular momentum of the disc about the origin is:
L=32MR2ω
Summary
The magnitude of the angular momentum of the disc about the origin is:
L=32MR2ω
---
Angular momentum L of a rotating body can be expressed as:
L=Iω
where I is the moment of inertia of the body and ω is the angular speed.
For a solid disc about its center of mass, the moment of inertia Icm is given by:
Icm=12MR2
Since we need the moment of inertia about the origin (which is a distance R away from the center of the disc), we will use the Parallel Axis Theorem. The theorem states:
I=Icm+Md2
where d is the distance from the center of mass to the new axis (in this case, d=R). Therefore, we have:
I=12MR2+MR2
I=12MR2+22MR2=32MR2
Now that we have the moment of inertia about the origin, we can substitute it into the angular momentum formula:
L=Iω=(32MR2)ω
Thus, the magnitude of the angular momentum of the disc about the origin is:
L=32MR2ω
The magnitude of the angular momentum of the disc about the origin is:
L=32MR2ω
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Mixed topics)
15 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Mixed Numerical Questions)
15 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1
45 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
A disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View SolutionA uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.

View Solution
A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.
View Solution
A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.
View SolutionA uniform disc of radius a and mass m, is rotating freely with angular speed ω in a horizontal plane about a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddenly attached to the rim of the disc of the disc and rotates with it. The new angular speed is
View SolutionA disc is freely rotating with an angular speed ω on a smooth horizontal plane. If it is hooked at a rigid pace P and rotates without bouncing about a point on its circumference. Its angular speed after the impact will be equal to.
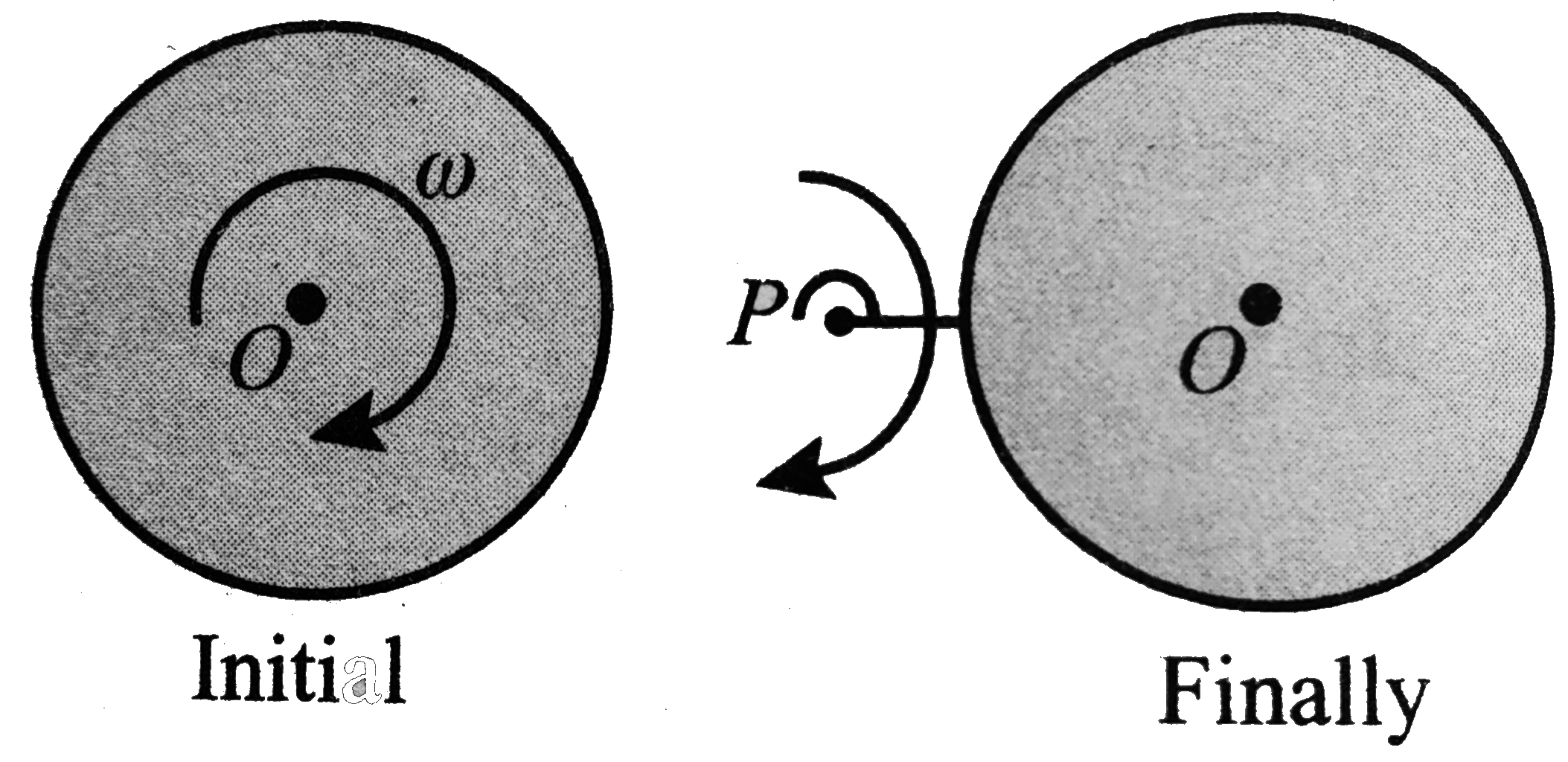
View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

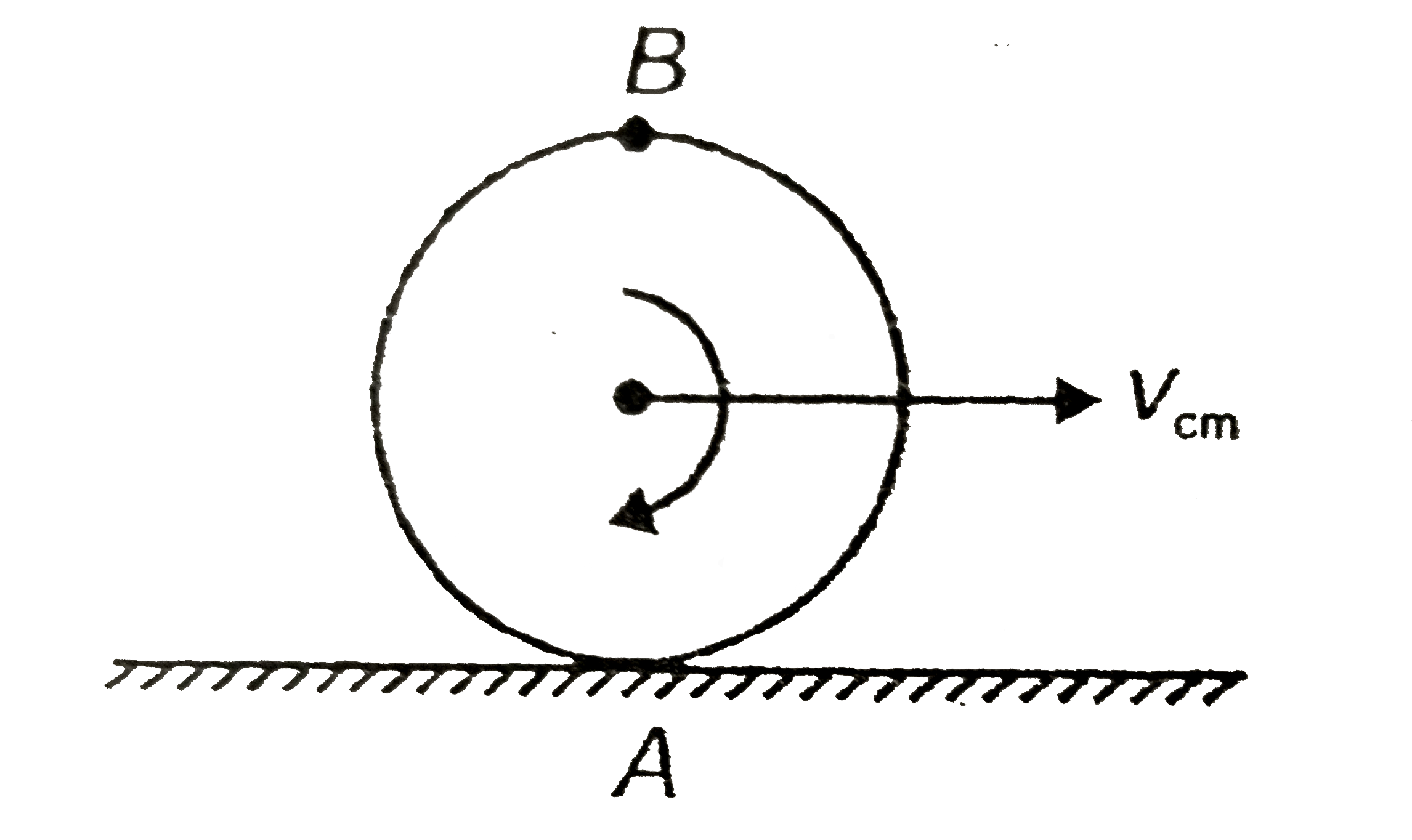
View SolutionA disc is undergoing rolling on a horizontal surface. Which of the statement about angular momentum of the disc is incorrect ?
View SolutionA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is

View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
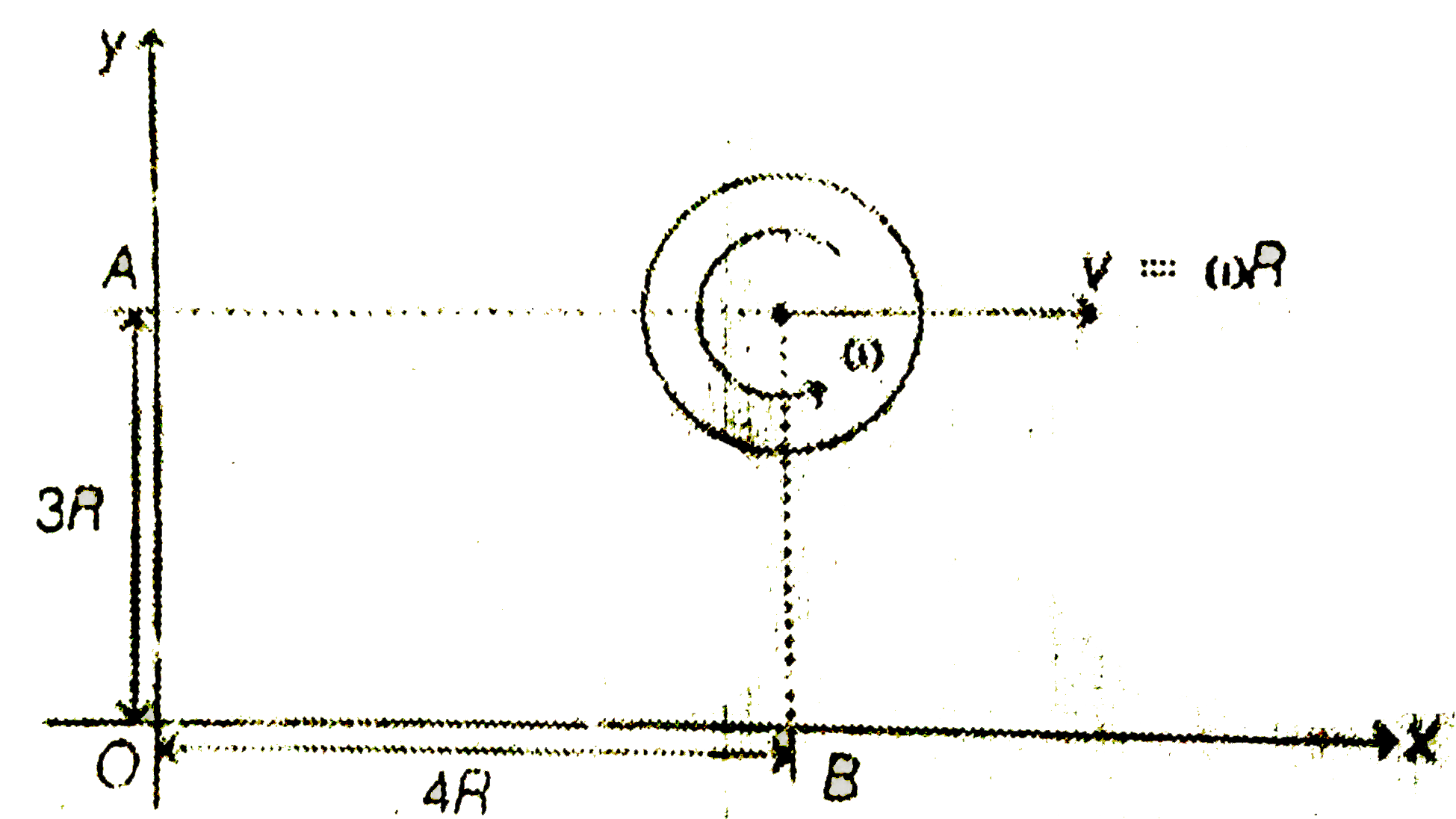
View Solution
