A uniform rod of mass M and length L, which is free to rotate about a fixed vertical axis through O, is lying on a frictionless horizontal table. A particle of equal mass strikes the rod with a velocity and sticks to it. The angular velocity of the combination immediately after the collision is:
The correct Answer is:C
To solve the problem step by step, we will use the principle of conservation of angular momentum.
1. Identify the System:
We have a uniform rod of mass M and length L that is free to rotate about a fixed vertical axis at point O. A particle of mass M (equal to the mass of the rod) strikes the rod with an initial velocity V0 and sticks to it.
2. Initial Angular Momentum:
Before the collision, the particle has linear momentum, which can be converted to angular momentum about point O. The distance from point O to the point of impact (the center of the rod) is L2. The initial angular momentum Li of the system is given by:
Li=mv0⋅r=MV0⋅L2
where m=M is the mass of the particle and r=L2 is the distance from point O to the center of the rod.
3. Final Angular Momentum:
After the collision, the rod and the particle rotate together with an angular velocity ω. The moment of inertia I of the system (rod + particle) about point O needs to be calculated. The moment of inertia of the rod about point O is given by:
Irod=13ML2
The particle, which is now at a distance L2 from point O, contributes to the moment of inertia as:
Iparticle=M(L2)2=ML24
Thus, the total moment of inertia If of the system after the collision is:
If=Irod+Iparticle=13ML2+ML24
4. Combine the Moments of Inertia:
To combine the moments of inertia, we need a common denominator:
If=412ML2+312ML2=712ML2
5. Conservation of Angular Momentum:
According to the conservation of angular momentum:
Li=Lf
Therefore:
MV0⋅L2=If⋅ω
Substituting If:
MV0⋅L2=712ML2⋅ω
6. Solve for Angular Velocity ω:
Cancel M from both sides (assuming M≠0):
V0⋅L2=712L2⋅ω
Rearranging gives:
ω=V0⋅L2712L2=V0⋅67L
Simplifying:
ω=6V07L
Final Answer:
The angular velocity of the combination immediately after the collision is:
ω=6V07L
We have a uniform rod of mass M and length L that is free to rotate about a fixed vertical axis at point O. A particle of mass M (equal to the mass of the rod) strikes the rod with an initial velocity V0 and sticks to it.
Before the collision, the particle has linear momentum, which can be converted to angular momentum about point O. The distance from point O to the point of impact (the center of the rod) is L2. The initial angular momentum Li of the system is given by:
Li=mv0⋅r=MV0⋅L2
where m=M is the mass of the particle and r=L2 is the distance from point O to the center of the rod.
After the collision, the rod and the particle rotate together with an angular velocity ω. The moment of inertia I of the system (rod + particle) about point O needs to be calculated. The moment of inertia of the rod about point O is given by:
Irod=13ML2
The particle, which is now at a distance L2 from point O, contributes to the moment of inertia as:
Iparticle=M(L2)2=ML24
Thus, the total moment of inertia If of the system after the collision is:
If=Irod+Iparticle=13ML2+ML24
To combine the moments of inertia, we need a common denominator:
If=412ML2+312ML2=712ML2
According to the conservation of angular momentum:
Li=Lf
Therefore:
MV0⋅L2=If⋅ω
Substituting If:
MV0⋅L2=712ML2⋅ω
Cancel M from both sides (assuming M≠0):
V0⋅L2=712L2⋅ω
Rearranging gives:
ω=V0⋅L2712L2=V0⋅67L
Simplifying:
ω=6V07L
The angular velocity of the combination immediately after the collision is:
ω=6V07L
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Mixed topics)
15 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Mixed Numerical Questions)
15 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1
45 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
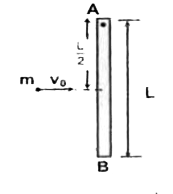
A uniform rod AB which is free to swing in the vertical plane about a horizontal axis through A, is hanging freely. A particle of equal mass strikes the rod with a velocity v0 and gets stucks to it. Find the angular velocity of the combination immediately after the collision.
View SolutionA wooden log of mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision aboutO.

View SolutionA thin bar of mass M and length L is free to rotate about a fixed horizontal axis through a point at its end. The bar is brought to a horizontal position and then released. The axis is perpendicular to the rod. The angular velocity when it reaches the lowest point is
View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View SolutionA Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
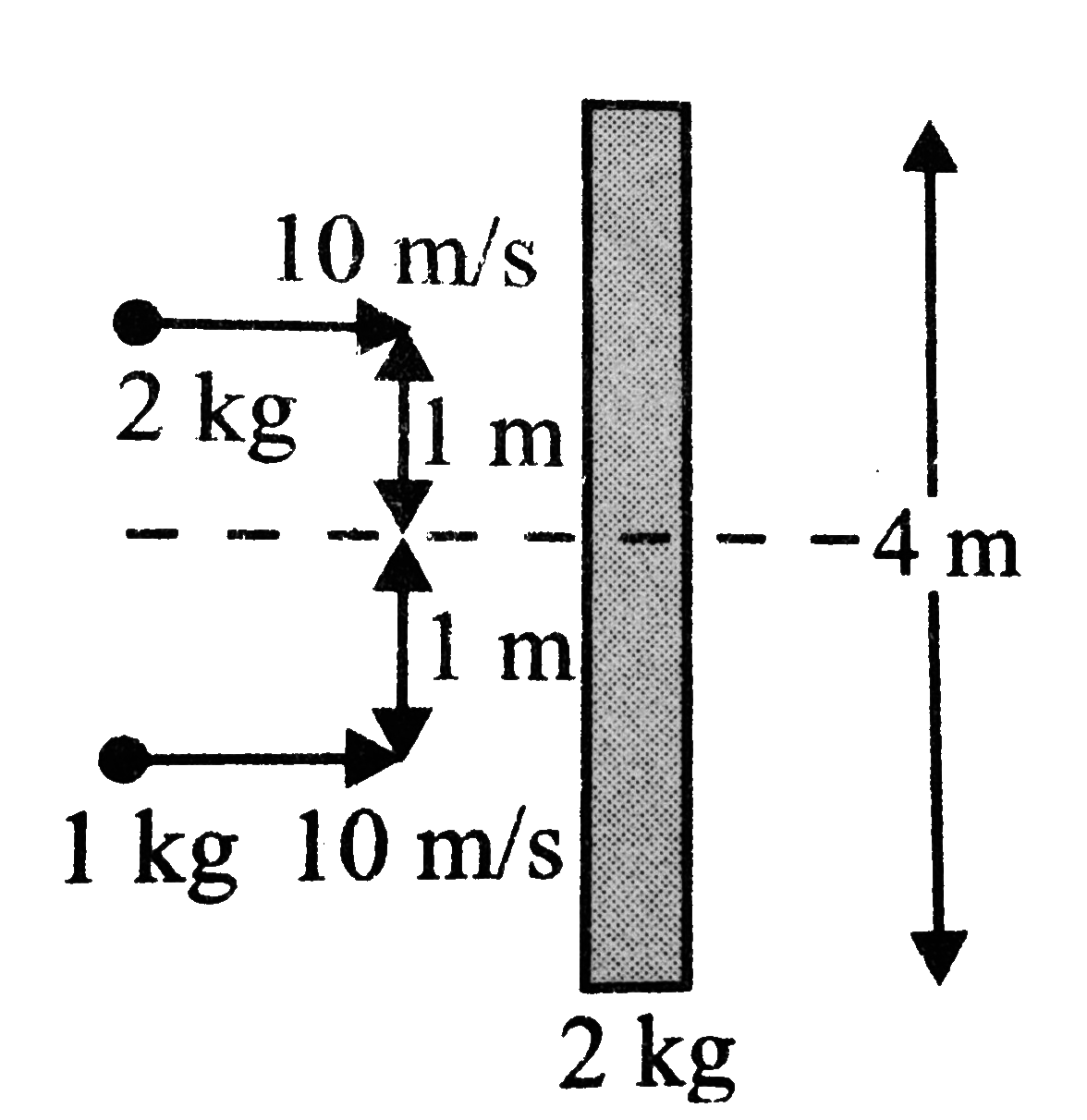
Angular velocity of the rod after collision is
View Solution
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View SolutionA uniform rectangular plate of mass m which is free to rotate about the smooth vwerticle hinge passing through the centre and perpendicular to the plate, is lying on a smooth horizontal surface. A particle of mass m is moving with speed 'u' collides with the plate and sticks to it as shown in figure. The angular velocity of the platye after colli9sion will be

View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionA Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
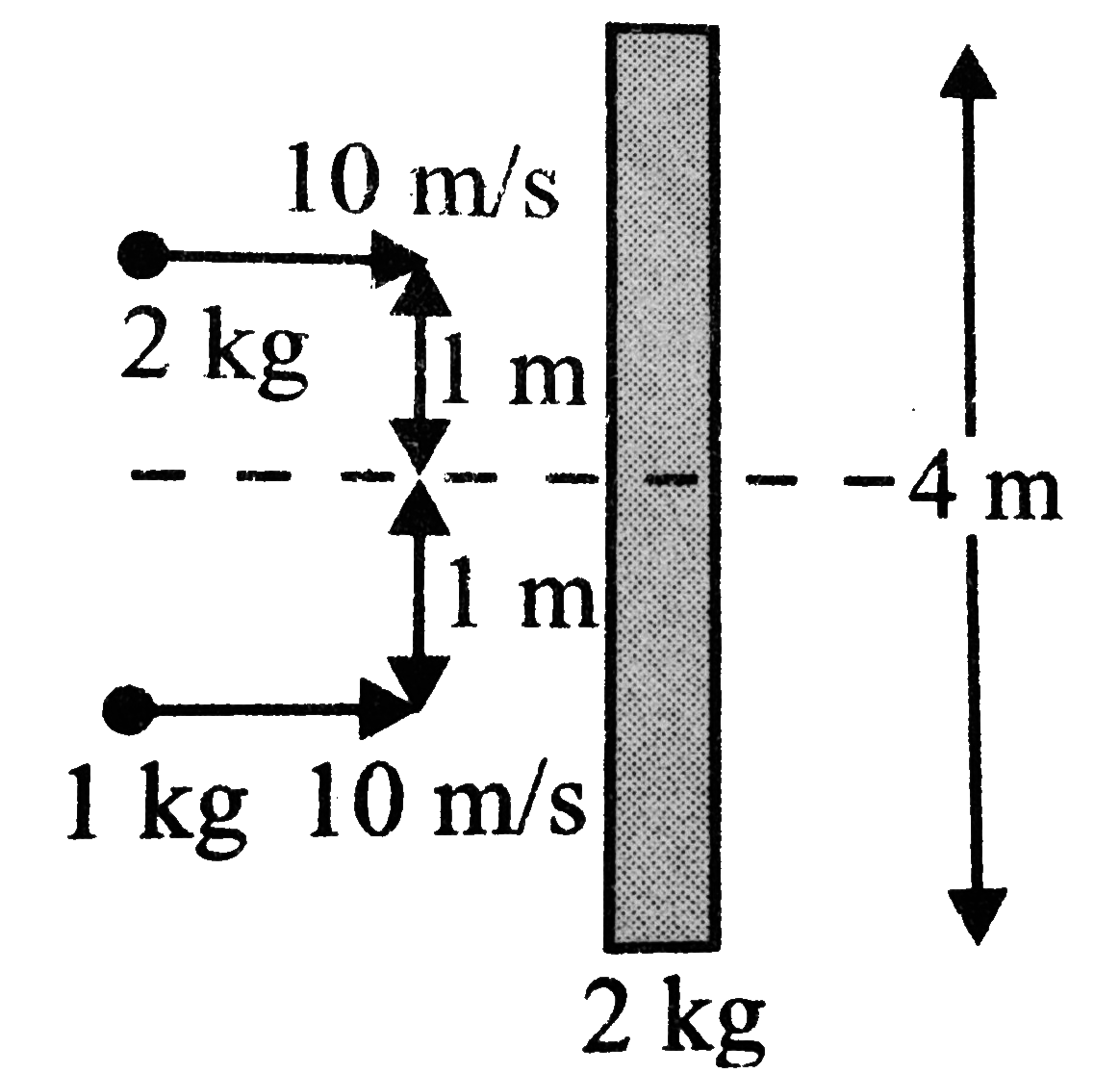
Velocity of the centre of mass of the rod after collision is
View Solution
