A smooth uniform, string of natural length , cross-sectional area and Young’s modulus is pulled along its length by a force on a horizontal surface. Find the elastic potential energy stored in the string.
The correct Answer is:
To find the elastic potential energy stored in a smooth uniform string of natural length l, cross-sectional area A, and Young’s modulus Y when it is pulled by a force F, we can follow these steps:
1. Understanding the Problem:
We have a string with natural length l, cross-sectional area A, and Young's modulus Y. When a force F is applied, the string stretches, and we need to find the elastic potential energy stored in it.
2. Tension in the String:
Consider a point at a distance x from one end of the string. The tension T at this point due to the force F can be expressed as:
T=F⋅xl
3. Stress in the String:
The stress σ at this point can be calculated using the formula:
σ=TA=F⋅xA⋅l
4. Elastic Potential Energy Formula:
The elastic potential energy U stored in the string can be calculated using the formula:
U=12Y∫σ2dv
where dv is the differential volume element. For a length dx of the string, dv=Adx.
5. Substituting Stress into the Energy Formula:
Substitute the expression for stress σ into the energy formula:
U=12Y∫l0(F⋅xA⋅l)2Adx
6. Simplifying the Integral:
This simplifies to:
U=12Y⋅F2A2l2∫l0x2dx
The integral ∫l0x2dx can be calculated as:
∫l0x2dx=l33
7. Final Calculation:
Plugging this back into the equation for U:
U=12Y⋅F2A2l2⋅l33
Simplifying this gives:
U=16⋅F2AY
Final Result:
The elastic potential energy stored in the string is:
U=16⋅F2AY
We have a string with natural length l, cross-sectional area A, and Young's modulus Y. When a force F is applied, the string stretches, and we need to find the elastic potential energy stored in it.
Consider a point at a distance x from one end of the string. The tension T at this point due to the force F can be expressed as:
T=F⋅xl
The stress σ at this point can be calculated using the formula:
σ=TA=F⋅xA⋅l
The elastic potential energy U stored in the string can be calculated using the formula:
U=12Y∫σ2dv
where dv is the differential volume element. For a length dx of the string, dv=Adx.
Substitute the expression for stress σ into the energy formula:
U=12Y∫l0(F⋅xA⋅l)2Adx
This simplifies to:
U=12Y⋅F2A2l2∫l0x2dx
The integral ∫l0x2dx can be calculated as:
∫l0x2dx=l33
Plugging this back into the equation for U:
U=12Y⋅F2A2l2⋅l33
Simplifying this gives:
U=16⋅F2AY
The elastic potential energy stored in the string is:
U=16⋅F2AY
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Single Correct
Explore 112 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Multiple Correct
Explore 17 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Exercise 5.3
Explore 9 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
Similar Questions
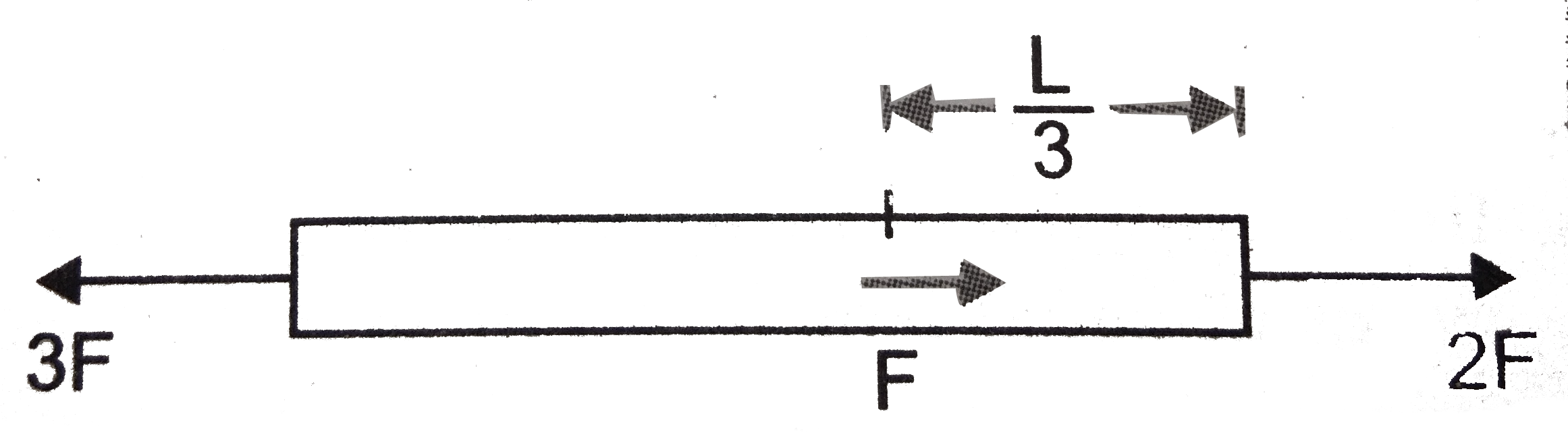
A uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :
View Solution
Knowledge Check
A wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
AYAx22LBYAx2L2CYAx2LDYAx2L
A uniform copper bar of density ρ , length L , cross - sectional area S and young's modulus Y is moving horizontally on a frictionless surface with constant acceleration a0. Find
(a) the stress at the center of the wire ,
(b) total elongation of the wire .
View SolutionA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View SolutionA uniform rod of length 2L, area of cross - section A and Young's modulus Y is lying at rest under the action of three forces as shown.
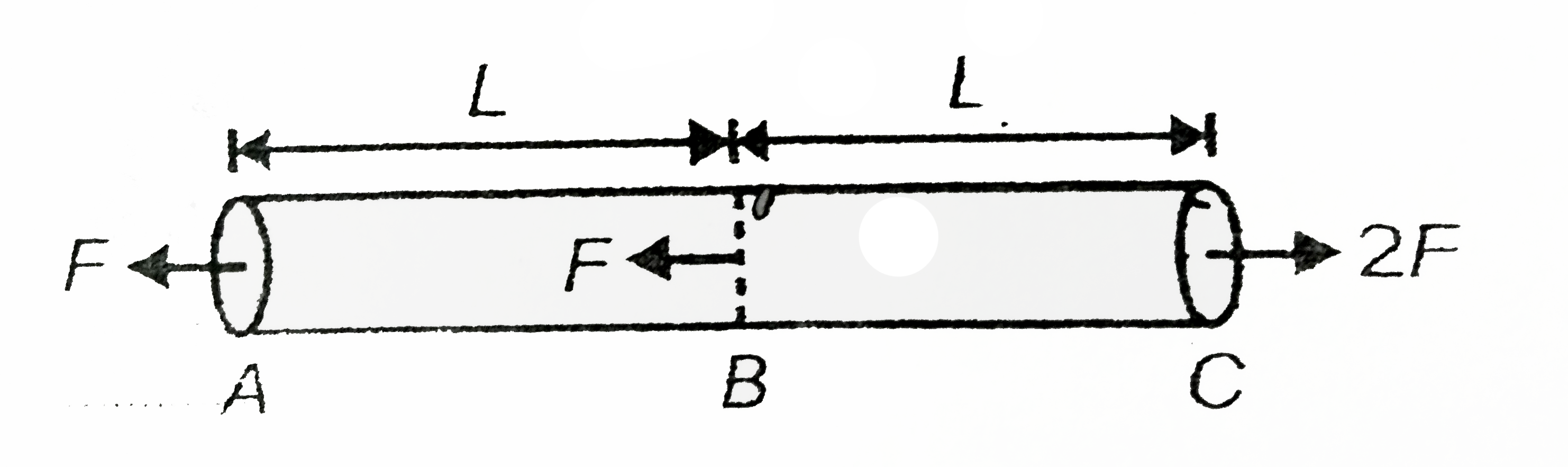
Select the correct alternatives.
View SolutionA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View SolutionA force F doubles the length of wire of cross-section a The Young modulus of wire is
View SolutionA uniform ring having mass m, radius R, cross section area of the wire A and young’s modulus Y is rotating with an angular speed ω(ω is small) on a smooth horizontal surface. Which of the following options is correct :
View SolutionA metallic rod of length l and cross-sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y,then the work done is proportional to
View Solution