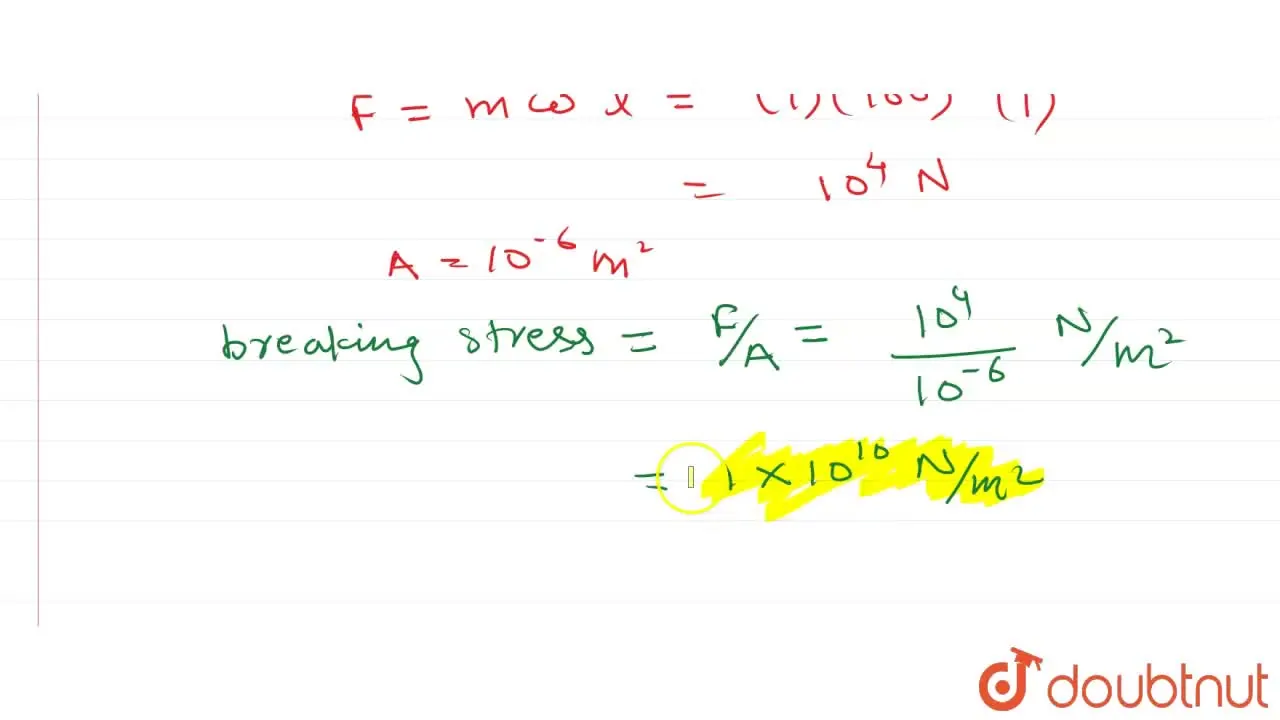A copper wire of negligible mass, 1m length and cross-sectional area 10−6m2 is kept on a smooth horizontal table with one end fixed. A ball of mass 1kg is attached to the other end. The wire and the ball are rotating with an angular velocity of 20rad/s. If the elongation in the wire is 10−3m.
a. Find the Young's modulus of the wire (in terms of ×1011N/m2).
b. If for the same wire as stated above, the angular velocity is increased to 100rad/s and the wire breaks down, find the breaking stress (in terms of ×1010N/m2).
The correct Answer is:1
The restoring froce (F) produced in the wire provides the necessary centripetal force i.e.
F=MLω2…………i
(since radius of circular path = length of wire =L)
We have Young's modulus
Y=F/A△L/L or F=YA,△LL………….ii
comparing eqn i and we get
YA△LL=mLω2 or Y=mL2ω2A△L
Substituting given values we get
Y=400×109=4×1011N/m2
The breaking force
F=mLω2max=(1kg)(1m)(100rad/s)2=104 newton
Therefore breaking stress= Breaking force)/ Area
=10410−6=1010N/m2
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Single Correct112videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Multiple Correct17videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.39videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
Similar Questions
A copper wire of negligible mass, length l and corss-section A is kept on a smooth horizontal table with one end fixed. A ball of mass m is attached to the other end. The wire and the ball are rotating with an angular velocity ω. If elongation in the wire is Δl, obtain the expression for the Young's modulus.
mL2ωAΔL
mω2L2AΔL
mω2LAΔL
mωLAΔLView SolutionThe area of a cross-section of steel wire is 0.1cm−2 and Young's modulus of steel is 2x1011Nm−2. The force required to stretch by 0.1% of its length is
View SolutionYoung.s modulus of a wire is 2×1011N/m2. If a stress of 2 x 108 N/m2 is applied at the free end of a wire, find the strain in the wire.
View SolutionA body of mass M is attached to the lower end of a metal wire, whose upper end is fixed . The elongation of the wire is l.
View SolutionA wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
View SolutionCalculate the force required to incrase the length of wire of cross-sectional area 10−6m2 by 50% if the Young's modulus of the material of the wire is 90×109Pa.
View SolutionA steel wire of 1.5 m long and of radius 1 mm is attached with a load 3 kg at one end the other end of the wire is fixed it is whirled in a vertical circle with a frequency 2 Hz. Find the elongation of the wire when the weight is at the lowest position Y=2×1011N/m2 and (g=10m/s2)
View SolutionA force F doubles the length of wire of cross-section a The Young modulus of wire is
View Solution_E01_080_Q01.png)
A copper wire of length 3 m and area of cross-section 1mm2 passes through an arrangement of two friction-less pulleys P1 and P2. One end of the wire is rigidly clamped and a mass of 1 kg is hanged from the other end if the young's modulus for copper is 10×1010N/m2 , then the elongation in the wire isView SolutionThe adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .
 View Solution
View Solution