A body of mass M is attached to the lower end of a metal wire, whose upper end is fixed . The elongation of the wire is l.
Loss in gravitational potential energy ofM is Mgl
The elastic potential energy stored in the wire is Mgl
The elastic potential energy stored in the wire is 12Mgl
Heat produced is 12Mgl
The correct Answer is:A, C, D
To solve the problem, we need to analyze the situation of a mass M attached to a metal wire and the elongation l of the wire. We will calculate the loss in gravitational potential energy, the elastic potential energy stored in the wire, and the heat produced.
1. Determine the Loss in Gravitational Potential Energy:
- When the mass M is attached to the wire, it falls a distance equal to the elongation l.
- The loss in gravitational potential energy ΔU can be calculated using the formula:
ΔU=Mgl
where g is the acceleration due to gravity.
2. Calculate the Elastic Potential Energy Stored in the Wire:
- The elastic potential energy Ue stored in the wire when it is stretched can be expressed as:
Ue=12Fl
- Here, F is the force applied, which is equal to the weight of the mass M:
F=Mg
- Substituting F into the elastic potential energy formula gives:
Ue=12(Mg)l=12Mgl
3. Determine the Heat Produced:
- According to the law of conservation of energy, the loss in gravitational potential energy is equal to the sum of the elastic potential energy stored in the wire and the heat produced.
- Therefore, we can write:
ΔU=Ue+Q
- Rearranging gives us the heat produced Q:
Q=ΔU−Ue
- Substituting the values we have:
Q=Mgl−12Mgl=12Mgl
Summary of Results:
- Loss in gravitational potential energy: Mgl
- Elastic potential energy stored in the wire: 12Mgl
- Heat produced: 12Mgl
- When the mass M is attached to the wire, it falls a distance equal to the elongation l.
- The loss in gravitational potential energy ΔU can be calculated using the formula:
ΔU=Mgl
where g is the acceleration due to gravity.
- The elastic potential energy Ue stored in the wire when it is stretched can be expressed as:
Ue=12Fl
- Here, F is the force applied, which is equal to the weight of the mass M:
F=Mg
- Substituting F into the elastic potential energy formula gives:
Ue=12(Mg)l=12Mgl
- According to the law of conservation of energy, the loss in gravitational potential energy is equal to the sum of the elastic potential energy stored in the wire and the heat produced.
- Therefore, we can write:
ΔU=Ue+Q
- Rearranging gives us the heat produced Q:
Q=ΔU−Ue
- Substituting the values we have:
Q=Mgl−12Mgl=12Mgl
- Loss in gravitational potential energy: Mgl
- Elastic potential energy stored in the wire: 12Mgl
- Heat produced: 12Mgl
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 Comprehension Based
6 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 Subjective
10 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 Single Correct
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
A body of mass M is attached to lower end of a metal wire whose upper End is fixed. The elongation is l. The ratio of loss of gravitational potential energy to the energy stored in the wire is
View SolutionA body of mass m is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1kg, the time period of oscillations becomes 5s. The value of m in kg is
View Solution
Knowledge Check
A metal wire of length L1 and area of cross section A is attached to a rigid support. Another metal wire of length L2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y1 and Y2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
A[(Y1Y2)A][2(Y1L2+Y2L1)]B[(Y1Y2)A](L1L2)2C[(Y1Y2)A](Y1L2+Y2L1)D[(Y1Y2)1/2A](L2+L1)1/2A metal wire of length L1 and area of cross section A is ttached to a rigid support. Another metal wire of length L2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y1 and Y2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
AY1Y2A2(Y1L2+Y2L1)BY1Y2A(L1L2)1/2CY1Y2A(Y1L2+Y2L1)D(Y1Y2)1/2A(L1L2)1/2
A body of mass m is atteched to the lower end of a spring whose upper end is fixed .The spring has negaligible mass .When the mass m is slightly puylled down and released it oscillation with a time period of 3s when the mass m is increased by 1kg time period of oscillations becomes 5s The value of m in kg is
View SolutionA ball of mass m is attached to the lower end of a vertical string whose upper end is fixed. An identcial ball 'B' moving with a velocity v0=6m/s at an angle θ=45∘ from vertical collides elastically with the ball 'A' as shown.
The verocity of the ball 'B' just after collision is
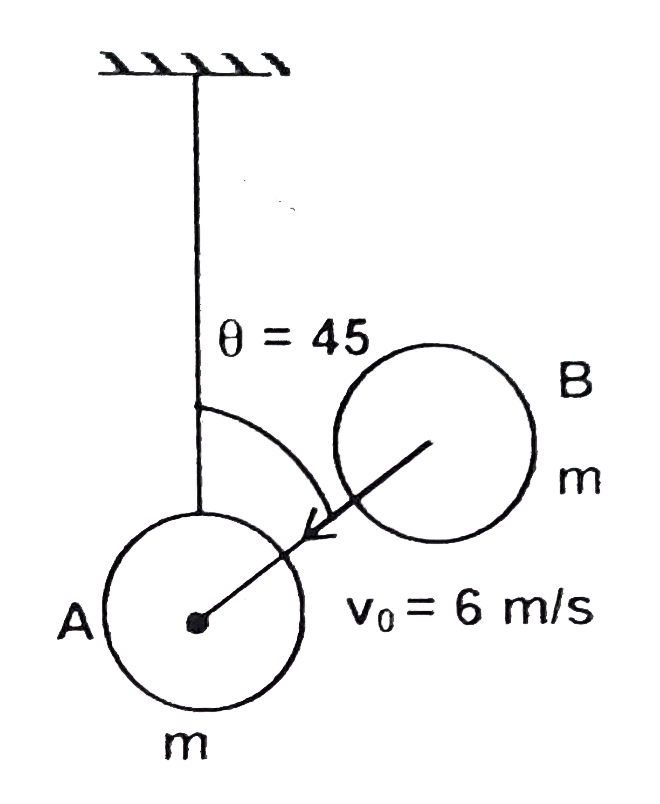
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View SolutionA ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x.
View SolutionA uniform cubical block of mass M is attached to a pulley. One end of a string, passing over the pulley is fixed to a light pole while is fixed on the bigger block and its another end is attached to a block of mass m as shown in figure. The maximum value of the mass m so that the block does not topple is : (string and pulley are ideal)

View Solution
System is shown in the figure. Velocity of sphere A is 9 ms. Find the speed of sphere B.
View Solution
