A steel rod of cross-sectional area and two brass rods each of cross-sectional area together support a load of as shown in the figure. ( Given, . Choose the correct option(s).

Stress in brass rod
Stress in steel rod
Stress in brass rod
Stress in steel rod
The correct Answer is:A, B
Area of steel rod , ltbr> Area of two brass rods ,
Stress in steel
and Stress in brass
Decrease in length of steel rod = Decrease in length of brass rod
or
...(i)
Now,
or ...(ii)
From Eqs. (i) and (ii) , we get
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 Comprehension Based
6 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 Subjective
10 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 Single Correct
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
A light rod of length of length 2m is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section 10−3m2 and the other is of brass of cross- section 2×10−3m2.x is the distance from the steel wire end, at which a weight may be hung. Ysteel=2×1011PaandYbrass=1011Pa
Which of the following statement(s) is /are correct ?
View SolutionA light rod of length of length 2m is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section 10−3m2 and the other is of brass of cross- section 2×10−3m2.x is the distance from the steel wire end, at which a weight may be hung. Ysteel=2×1011PaandYbrass=1011Pa
Which of the following statement(s) is /are correct ?
View Solution
Knowledge Check
The two femurs each of cross-sectional area 10cm2 support the upper part of a human body of mass 40 kg. the average pressure sustained by the femurs is (take g=10ms−2)
A2×102Nm−2B2×104Nm−2C2×105Nm−2D2×106Nm−2The self inductance of a solenoid that has a cross-sectional area of 1cm2, a length of 10 cm and 1000 turns of wire is
A0.86mHB1.06mHC1.26mHD1.46mHA light rod of length 2 m is suspended from ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 0.1 cm sq. and the other of brass of cross-section 0.2 cm sq. Along the rod at what distance a weight may be hung to produce equal stresses in the wires?
(YSteel=2×1011Nm−2,YBass=1×1011Nm−2)A43m from steel wireB43m from brass wireC1 m from steel wireD14m from brass wire
The two thigh bones each of cross-sectional area 15cm2 support the upper part of a person of mass 70 kg. The pressure sustained by these thigh bones is
View SolutionA piston of cross-sectional area 100cm2 is used in a hydraulic pressure to exert a force of 107 dyne on the water. The cross-sectional area of the other piston which support a truck of mass 2000 kg is
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
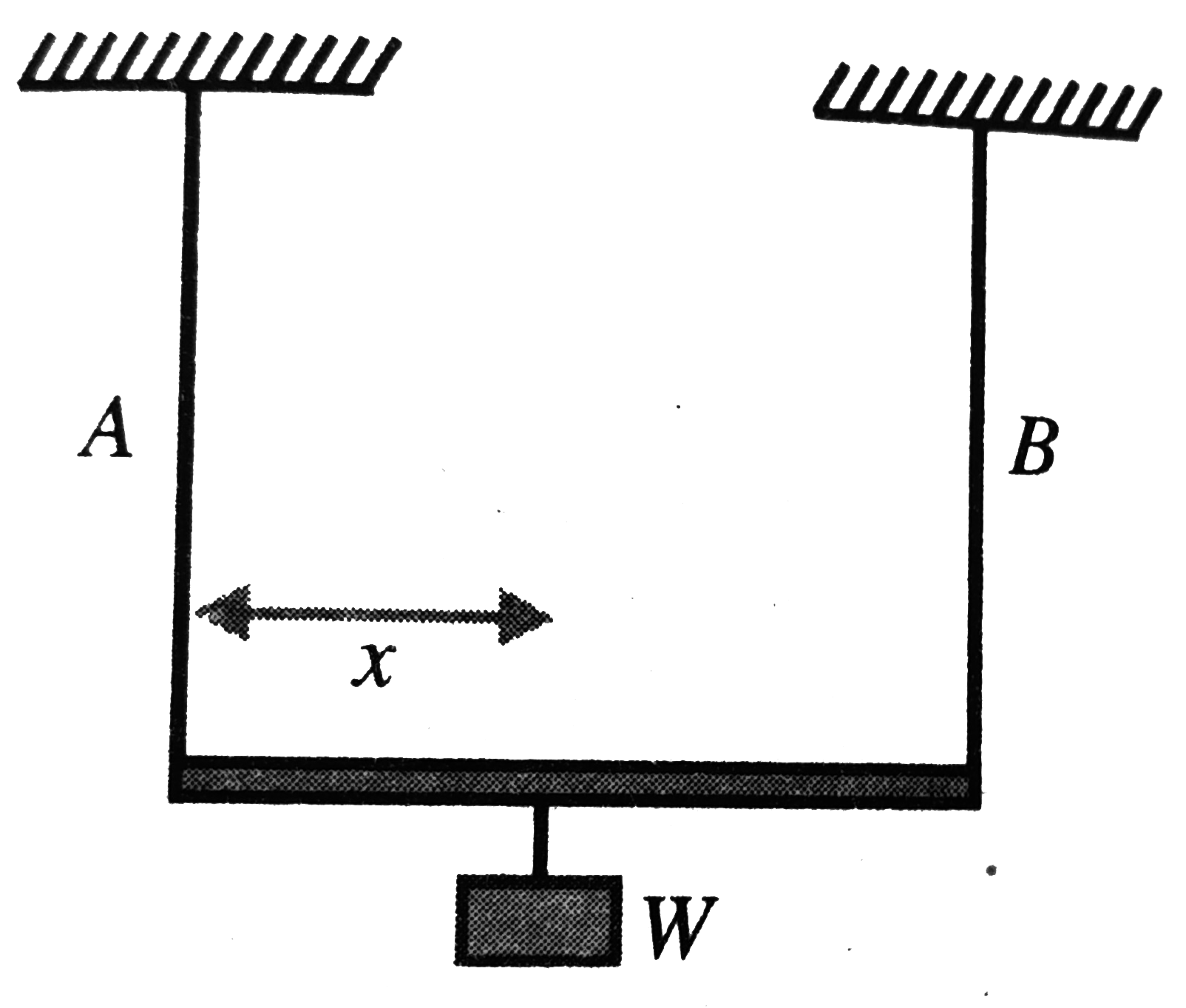
Determine the value of x so that equal stresses are produced in each wire.
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
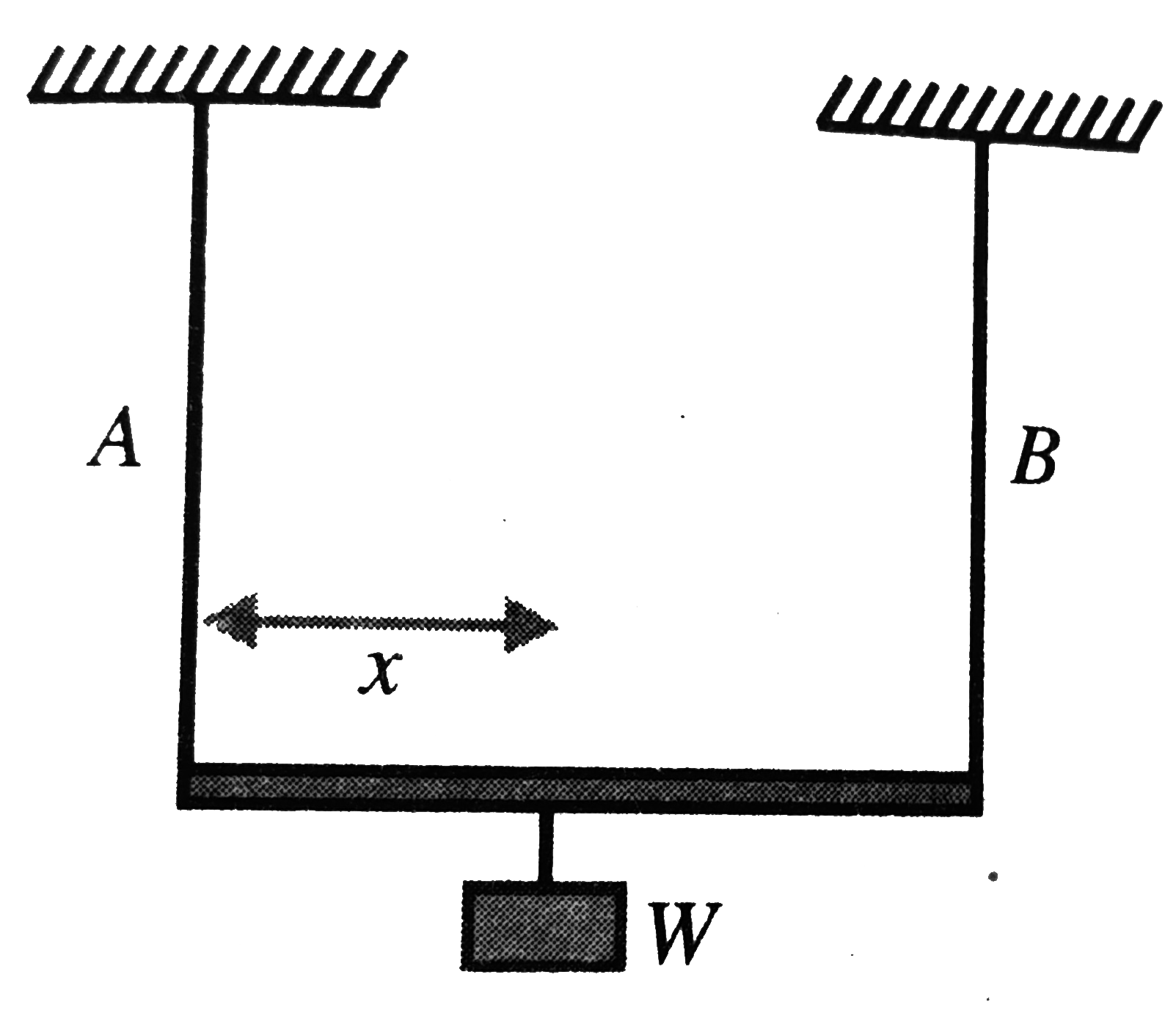
Determine the value of x so that equal strains are produced in each wire
View SolutionThe two thigh bones (femur bones) each of cross-sectional area 10cm2 support the upper part of a human body of mass 40 kg . Estimate the average pressure sustained by the femurs. g=10m/s2
View Solution
