A body of mass is atteched to the lower end of a spring whose upper end is fixed .The spring has negaligible mass .When the mass is slightly puylled down and released it oscillation with a time period of when the mass is increased by time period of oscillations becomes The value of in is
The correct Answer is:D
To solve the problem step by step, we will use the formula for the time period of a mass-spring system and set up equations based on the information given.
Step 1: Write the formula for the time period of a spring-mass system.
The time period T of a mass-spring system is given by the formula:
T=2π√mk
where m is the mass attached to the spring and k is the spring constant.
Step 2: Set up the first equation using the initial mass m.
According to the problem, when the mass is m, the time period is 3 seconds. Thus, we can write:
3=2π√mk
Step 3: Rearrange the first equation to express mk.
Squaring both sides gives:
9=4π2mk
Rearranging this, we find:
mk=94π2(Equation 1)
Step 4: Set up the second equation using the increased mass m+1.
When the mass is increased by 1 kg, the time period becomes 5 seconds. Thus, we can write:
5=2π√m+1k
Step 5: Rearrange the second equation to express m+1k.
Squaring both sides gives:
25=4π2m+1k
Rearranging this, we find:
m+1k=254π2(Equation 2)
Step 6: Set up a ratio of the two equations.
Now, we can set up a ratio of Equation 1 and Equation 2:
mkm+1k=9/4π225/4π2
This simplifies to:
mm+1=925
Step 7: Cross-multiply to solve for m.
Cross-multiplying gives:
25m=9(m+1)
Expanding this results in:
25m=9m+9
Subtracting 9m from both sides gives:
16m=9
Step 8: Solve for m.
Dividing both sides by 16 gives:
m=916 kg
Final Answer:
The value of m is 916 kg.
---
The time period T of a mass-spring system is given by the formula:
T=2π√mk
where m is the mass attached to the spring and k is the spring constant.
According to the problem, when the mass is m, the time period is 3 seconds. Thus, we can write:
3=2π√mk
Squaring both sides gives:
9=4π2mk
Rearranging this, we find:
mk=94π2(Equation 1)
When the mass is increased by 1 kg, the time period becomes 5 seconds. Thus, we can write:
5=2π√m+1k
Squaring both sides gives:
25=4π2m+1k
Rearranging this, we find:
m+1k=254π2(Equation 2)
Now, we can set up a ratio of Equation 1 and Equation 2:
mkm+1k=9/4π225/4π2
This simplifies to:
mm+1=925
Cross-multiplying gives:
25m=9(m+1)
Expanding this results in:
25m=9m+9
Subtracting 9m from both sides gives:
16m=9
Dividing both sides by 16 gives:
m=916 kg
The value of m is 916 kg.
Similar Questions
A body of mass m is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1kg, the time period of oscillations becomes 5s. The value of m in kg is
View SolutionA body of mass M is attached to the lower end of a metal wire, whose upper end is fixed . The elongation of the wire is l.
View SolutionA body of mass m attached to a spring which is oscillating with time period 4 s. If the mass of the body is increased by 4 kg, its time period increases by 2 s. Determine value of initial mass m.
View SolutionA mass M is suspended from a spring of negiliglible mass the spring is pulled a little and then released so that the mass executes simple harmonic oscillation with a time period T If the mass is increases by m the time period because (54T),The ratio of mM is
View SolutionA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be
 View Solution
View SolutionA mass M attached to a spring oscillation with a period of 2s. If the mass is increased by 2kg , the period increases by 1s, find the initial mass m assuming that Hooke's law is obeyed.
View SolutionA mass M is suspended from a spring of negligible mass. The spring is pulled a little then released, so that the mass executes simple harmonic motion of time period T. If the mass is increased by m, the time period becomes 5T3. Find the ratio of m/M.
View SolutionThe time period of small oscillations of mass m :-
_S01_040_Q01.png) View Solution
View Solution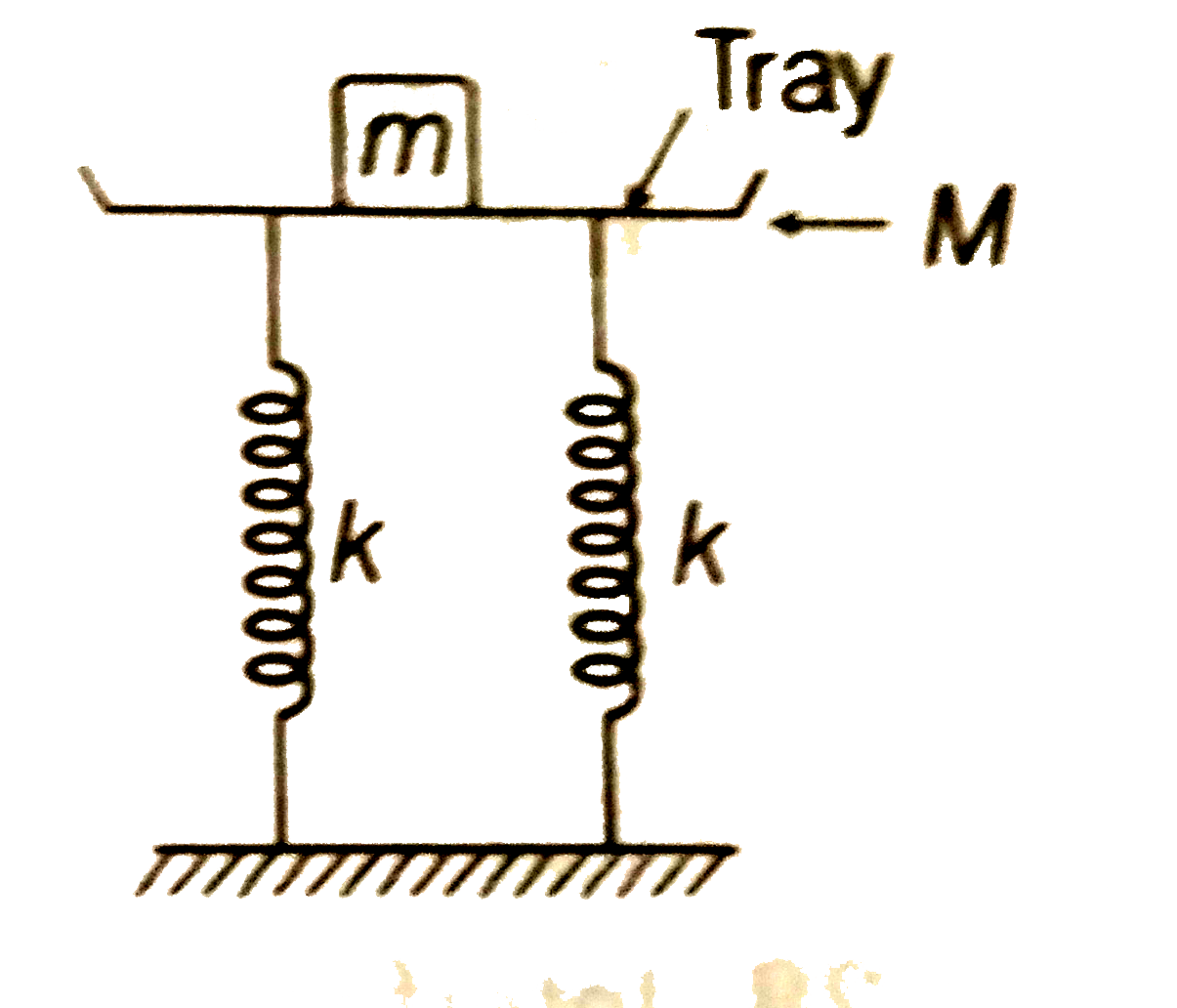
A tray of mass M=10kg is supported on two identical springs, each of spring constant k, as shown in figure, when the tray is depressed a little and released, it executes simple harmonic motion of period 1.5 s. when a block of mass m is placed on the tray, the speed of oscillation becomes 3 s. the value of m isView SolutionWhen a mass m attached to a spring it oscillates with period 4s. When an additional mass of 2 kg is attached to a spring, time period increases by 1s. The value of m is :-
View Solution
