The time period of small oscillations of mass m :-
_S01_040_Q01.png)
2π√m6k
2π√11m6K
2π√6m11K
2π√mK
The correct Answer is:B
Equivalent spring constant 1Keq=13K+12K+1K⇒Keq=6K11∴T2π√mKeq=2π√11m6K
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES
29 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01
117 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
24 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A light pulley is suspended at the lower end of a spring of constant k1, as shown in figure. An inextensible string passes over the pulley. At one end of string a mass m is suspended, the other end of the string is attached to another spring of constant k2. The other ends of both the springs are attached to rigid supports, as shown. Neglecting masses of springs and any friction, find the time period of small oscillations of mass m about equilibrium position.

View SolutionA system is shown in the figure. The force The time period for small oscillations of the two blocks will be

View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:

View SolutionFind the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
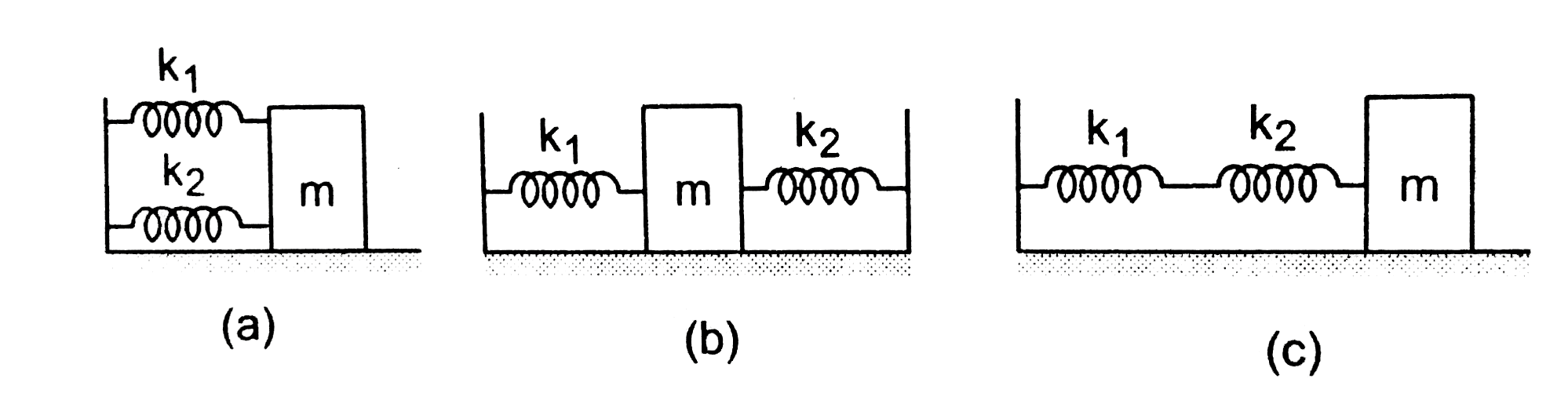
View SolutionA uniform plank of mass m, free to move in the horizontal direction only , is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attached to a fixed wall by mean of a light spring constant k. There is no slipping between the cylinder and the planck , and between the cylinder and the ground. Find the time period of small oscillation of the system.

View SolutionA thin fixed ring of radius 'R' and positive charge 'Q' is placed in a vertical plane. A particle of mass 'm' and negative charge 'q' is placed at the centre of ring. If the particle is given a small horizontal displacement, show that it executes SHM. Also find the time period of small oscillations of this particle, about the centre of ring. (Ignore gravity)
View SolutionA uniform stick of length l is mounted so as to rotate about a horizontal axis perpendicular to the stick and at a distance d from the centre of mass. The time period of small oscillation has a minimum value when d/l is
View SolutionThe ratio of the time periods of small oscillation of the insulated spring and mass system before and after charging the masses is
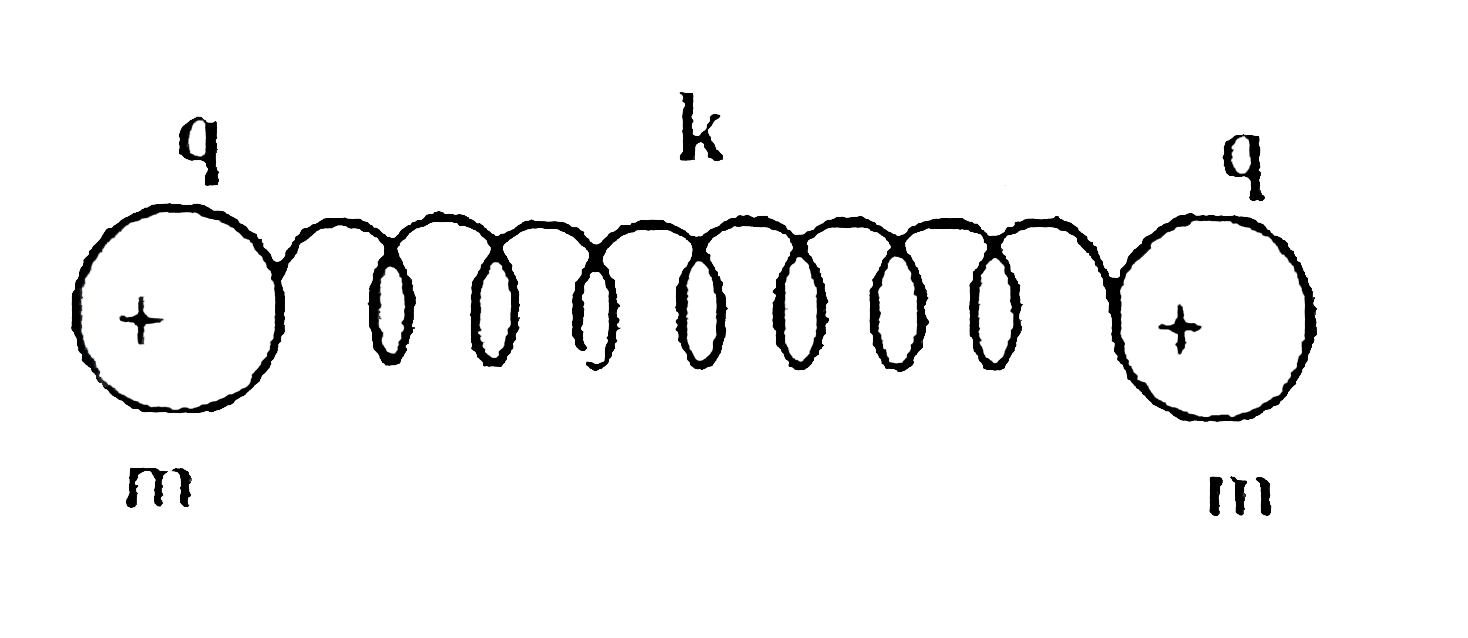
View SolutionIn the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.

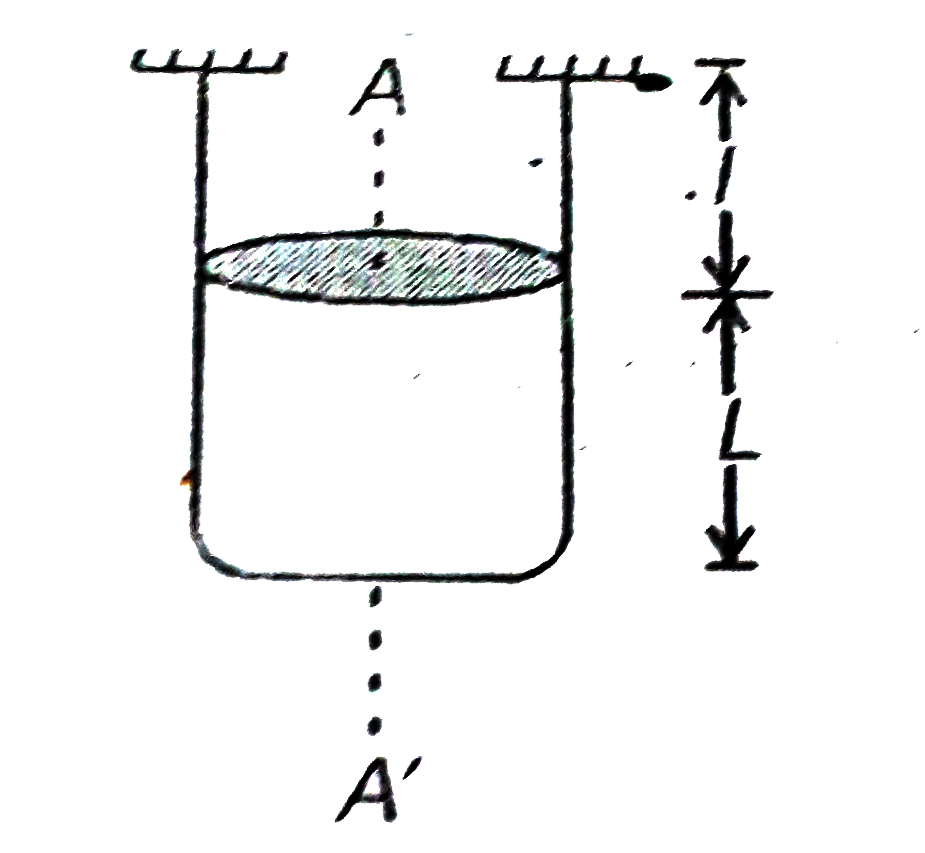
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
View Solution
